��Ŀ����
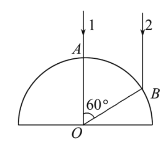
����Ŀ����ͼ��ʾ��������A��B��һ��ϵһ����Ϊm��0.1 kg��С����������һ�˷ֱ�̶������A��B���������������L��2 m��������ֱʱ����ļнǷֱ�Ϊ30���60����(g��10 m/s2)������
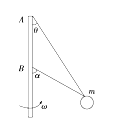
��1����B������ļн�Ϊ60�㣬������ǡ������ʱ��A��������Ϊ���
��2����С��Ľ��ٶ�����3 rad/sʱ�����ж�A��B������������������д���ж����ݡ�
��3�����ݵڣ�2����������жϽ�������������С��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]() ��
�� ![]()
����������1���������⣬������ǡ������ʱ�� ![]() ����
����![]() ��
��
(2)����������ֱʱ��A��B���������ֱ�Ϊ![]() ��С�������Ϊm��A������ֱ����ļн�Ϊ
��С�������Ϊm��A������ֱ����ļн�Ϊ![]() ��B������ֱ����ļн�Ϊ
��B������ֱ����ļн�Ϊ![]() ��
��
��B����ǡ������ʱ����С�����������������ţ�ٵڶ����ɵ�
ˮƽ����![]()
��ֱ����![]()
��������ʽ���![]() ��
��
��A����ǡ������ʱ
ˮƽ����![]()
��ֱ����![]()
��������ʽ����� ![]() ��
��
��![]() ������A��B��������������
������A��B��������������
��3����ֱ���� ![]()
ˮƽ���� ![]()
��ã� ![]() ��
�� ![]() ��
��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ