题目内容
均匀分布在地球赤道平面上空的三颗同步通信卫星够实现除地球南北极等少数地区外的全球通信.已知地球的半径为R,地球表面的重力加速度为g,地球的自转周期为T.关于三颗同步卫星中,任意两颗卫星间的弧长s的表达式为s=
.
| 2π |
| 3 |
| 3 |
| ||
| 2π |
| 3 |
| 3 |
| ||
分析:了解同步卫星的含义,即同步卫星的周期必须与地球相同.
通过万有引力提供向心力,列出等式通过已知量确定未知量.
根据万有引力等于重力,代换GM.
通过万有引力提供向心力,列出等式通过已知量确定未知量.
根据万有引力等于重力,代换GM.
解答:解:设同步卫星的轨道半经为r
根据:
=mg
得:GM=gR2
根据
=m
r
由以上两式得:r=
根据题意画出俯视三颗同步通信卫星的几何位置图象:
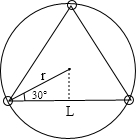
根据几何关系得:
S=
×2πr
得S=
则任意两颗卫星间的弧长s的表达式是
答:三颗卫星中任意两颗卫星间弧长s是
.
根据:
| GMm |
| R2 |
得:GM=gR2
根据
| GMm |
| r2 |
| 4π2 |
| T2 |
由以上两式得:r=
| 3 |
| ||
根据题意画出俯视三颗同步通信卫星的几何位置图象:

根据几何关系得:
S=
| 1 |
| 3 |
得S=
| 2π |
| 3 |
| 3 |
| ||
则任意两颗卫星间的弧长s的表达式是
| 2π |
| 3 |
| 3 |
| ||
答:三颗卫星中任意两颗卫星间弧长s是
| 2π |
| 3 |
| 3 |
| ||
点评:不同的同步卫星在地球赤道平面上空同一轨道上,画出几何图象,找出物理量的几何关系.
运用黄金代换式GM=gR2求出问题是考试中常见的方法.
运用黄金代换式GM=gR2求出问题是考试中常见的方法.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目