��Ŀ����
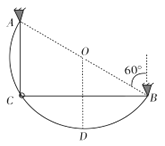
����Ŀ����ͼ����ʾ��һ��Ϊl=1m��������һ�˴��ڹ�O���ˮƽת���ϣ���һ�˹̶�һ����Ϊm=0.2kg��С������װ����O������ֱ����ת������ϵͳ����������ʹС��ͨ����ߵ���ٶȲ��ϼӿ죬ͨ����������С��ͨ����ߵ�ʱ������С�������F��С������ߵ㶯��Ek�Ĺ�ϵ��ͼ����ʾ���������ٶ�g=10m/s2 �� ������Ħ���Ϳ�����������������ش��������⣺
��1����ҪС������������Բ���˶�����С�����ߵ���ٶ��к�Ҫ�������и�������ĸ��ʾ��
��2���������Ŀ��ͼ���е����������ͼ����b����ʾ״̬С��Ķ��ܣ�
��3����С��ﵽͼ����b����ʾ״̬ʱ������ֹͣ�������룮֮����˶������У������������ﵽ���ֵ��λ��ʱ�������ϣ������˲�����������Ĵ�С��
���𰸡�
��1���⣺С��պ�ͨ����ߵ�������Բ�˶�Ҫ������ߵ��������㣺mg=m ![]() ��
��
���С�����ߵ���ٶ�Ҫ���㣺v�� ![]() ��
��
����ҪС������������Բ���˶�����С�����ߵ���ٶ����㣺v�� ![]() ��
��
��2���⣺С������ߵ�ʱ�У�mg+F=m ![]() ����Ϊ��EK=
������EK= ![]() mv2��
mv2��
��ͼ��֪��b��ʱF=4.0N��
��ã�EK=3.0J��
�����Դ�ϵͳ���Ĺ�Ϊ3.0J��
��3���⣺��ֹͣ��������֮��С����������������������������ֱ������Բ���˶����˶������л�е���غ㣮��С���˶�����͵�ʱ�����������ﵽ���ֵ��
��С������͵���ٶ�Ϊv���Դ�b״̬��ʼ���ﵽ��͵�Ĺ���Ӧ�û�е���غ㶨�ɣ��У�mg2l= ![]() mv2��EKb��
mv2��EKb��
������͵���������ΪFm����ţ�ٵڶ������У�Fm��mg=m ![]() ��
��
��ʽ������ã�Fm=16N��
��������˲�����������Ĵ�СΪ16N��
�𣺱���˲�����������Ĵ�СΪ16N��
����������1������ߵ㣬��ţ�ٵڶ����ɿ���С������������Բ���˶��������������2������ߵ㣬��ţ�ٵڶ����ɲ����ͼ����Ϣ����С�������Ͱ��߳��ȣ���ͼ���б�ʣ����ݶ��ܶ���������ϵͳ���Ĺ�����3��Ӧ�û�е���غ㶨�ɺ�ţ�ٵڶ����������˲�����������Ĵ�С��
�����㾫����������Ҫ���������������ܹ�ϵ�����֪ʶ�㣬��Ҫ��������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ������������ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1������ȷ�����⣮