题目内容
【题目】如图所示为一块半圆柱形玻璃砖,半圆形截面ABD的圆心为O,半径为R。现有平行光束平行ABD平面以入射角α=45°射到长度为L、宽为2R的长方形截面ABEF上,最终从下表面射出玻璃砖。已知玻璃的折射率n=![]() 。求
。求
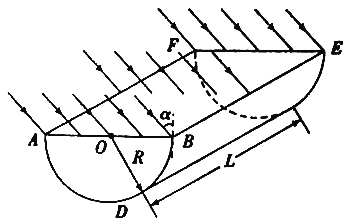
①光在ABEF界面的折射角β及全反射临界角C;
②玻璃砖下表面有光线射出部分的面积S。
【答案】30°,45° ![]()
【解析】①作出光路图,如图所示,
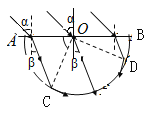
由折射定律,有:![]()
得:sinβ=![]() ,
,
解得:β=30°
根据![]() 解得
解得![]() ,则C=450
,则C=450
(2)如果光线AC刚好在C点发生全反射,则有:nsin∠ACO=sin90°,而n=![]() .
.
即有∠ACO=sin45°,
则∠AOC=75°
同理在右侧发生全反射的光线入射点为D,可解得∠BOD =15°
故能够从半圆柱球面上出射的光束范围限制在CD区域上,对应的角度为180°-75°-15°=90°,所以底面透光部分的弧长为:L′=![]() ×2πR=
×2πR=![]()
玻璃砖下表面有光线射出部分的面积![]()

【题目】某小组利用如下装置研究“一定质量气体温度不变时,压强与体积的关系”。
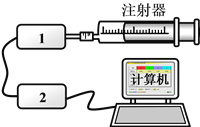
如图所示,带刻度的注射器内封闭了一定质量的气体,推动活塞可以改变气体体积V,实验所用测量压强的装置较特殊,测量的是注射器内部气体和外部大气(压强为P0)的压强差Δp,在多次改变体积后,得到如下数据:
Δp/×105pa | 0 | 0.11 | 0.25 | 0.43 | 0.67 |
V/mL | 10 | 9 | 8 | 7 | 6 |
(1)图中装置1为__________________,装置2为__________________。
(2)每次气体的状态调整后,都要等一会儿再记录数据,这是为了__________________。
(3)研究小组基于数据,以Δp为y轴,作出的函数图线为直线,则x轴是____________。
(4)若图像斜率为k,该直线的函数表达式是__________________,图像纵轴截距的绝对值的物理涵义是_____________________________。