题目内容
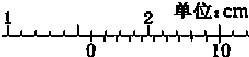（1）在测量重力加速度的实验中，某同学用一根细线和一均匀小球制成单摆．首先该同学用游标卡尺测出小球直径d 如图（a）所示，其读数为：16.0
16.0
mm，然后测单摆的周期，每经过最低点该同学就计数一次，且第一次计数为0，他已经测得计数为n次的总时间为t，则单摆的周期为：| 2t |
| n |
| 2t |
| n |
悬挂点到小球顶端的线长l
悬挂点到小球顶端的线长l
．将g用测得量符合表示，可得g=n2π2(l+
| ||
| t2 |
n2π2(l+
| ||
| t2 |
（2）另外一同学利用单摆根据公式测得的g=
| 4π2l |
| T2 |
DE
DE
．A．摆球质量过大 B．摆球振幅过小
C．测量摆长时忘记加上小球半径 D．将摆长当成了摆线长和球直径之和
E．摆动次数多记了一次．
分析：游标卡尺读数为主尺刻度与游标刻度之和，根据从单摆运动到最低点开始计时且记数为0，到第n次经过最低点所用的时间内为t，确定单摆全振动的次数，再求解周期，
由T=2π
可知，还需测量悬挂点到小球顶端的距离l；明确单摆的有效长度，代入T=2π
，从而可求加速度g，根据g的表达式可确定误差原因．
由T=2π
|
|
解答：解：（1）游标卡尺读数为主尺刻度与游标刻度之和，故为：主尺刻度为1.6cm，游标刻度为0×
mm，故读数为：16.0mm
由题，从单摆运动到最低点开始计时且记数为0，到第n次经过最低点所用的时间内为t，则单摆全振动的次数为：N=
周期：T=
=
由T=2π
，可知，还需测量悬挂点到小球顶端的距离l
单摆的长度为：L=l+
，
由单摆的周期公式：T=2π
得：g=
故联立上式，可解得：g=
（2）根据g=
A、B、g与摆球质量及振幅无关，故AB错误；
C、测量摆长忘记加上小球半径，则摆长变小，由上式可知g偏小，故C错误；
D、将摆长当成了摆线长和球直径之和，则L变大，故g偏大，故D正确；
E、摆动次数多记，则T偏小，故g偏大，故E正确
故选：DE
故答案为：（1）16.0；
；悬挂点到小球顶端的线长为l；
，（2）DE
| 1 |
| 10 |
由题，从单摆运动到最低点开始计时且记数为0，到第n次经过最低点所用的时间内为t，则单摆全振动的次数为：N=
| n |
| 2 |
周期：T=
| t |
| N |
| 2t |
| n |
由T=2π
|
单摆的长度为：L=l+
| d |
| 2 |
由单摆的周期公式：T=2π
|
得：g=
| 4π2L |
| T2 |
故联立上式，可解得：g=
n2π2(l+
| ||
| t2 |
（2）根据g=
n2π2(l+
| ||
| t2 |
A、B、g与摆球质量及振幅无关，故AB错误；
C、测量摆长忘记加上小球半径，则摆长变小，由上式可知g偏小，故C错误；
D、将摆长当成了摆线长和球直径之和，则L变大，故g偏大，故D正确；
E、摆动次数多记，则T偏小，故g偏大，故E正确
故选：DE
故答案为：（1）16.0；
| 2t |
| n |
n2π2(l+
| ||
| t2 |
点评：常用仪器的读数要掌握，这是物理实验的基础．掌握单摆的周期公式，从而求解加速度，摆长、周期等物理量之间的关系．单摆的周期采用累积法测量可减小误差．对于测量误差可根据实验原理进行分析．
练习册系列答案
相关题目
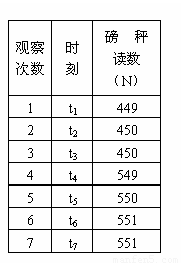
某学生想了解所居住高楼内电梯运行的大致规律，他设计一个利用称体重的磅秤来进行测量和研究的方案：