题目内容
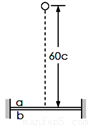
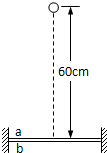
ab为紧靠着的、且两边固定的两张相同的薄纸,如图所示.一个质量为1kg的小球从距纸面高为60cm的地方自由下落,恰能穿破两张纸(即穿过后速度为零),则小球穿破纸的瞬间损失的机械能为 J.若将a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则a纸距离b纸不超过 cm.(设小球单独穿破一张纸所需的能量为几乎同时穿破二张纸所需能量的一半)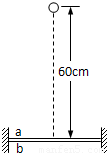
【答案】分析:下落的小球在重力做功下,将重力势能转化为动能,穿破两张纸后将动能转化为内能,通过动能定理来计算损失的机械能;要使小球仍能穿破两张纸,则根据动能定理可求出a纸距离b纸间距.
解答:解:当ab为紧靠着的、且两边固定的两张相同的薄纸,根据动能定理,则有:WG+Wf=0-0.
所以Wf=-WG=-1×10×0.6J=-6J,因此小球穿破两张纸的瞬间损失的机械能为6J.
a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则当小球的动能达到3J时,才能穿破纸张.
设释放点距a纸距离为L,根据动能定理,则有:mgL≥3J,解得:L≥30cm.因此a纸距离b纸不超过30cm.
故答案为:6;30.
点评:考查动能定理的应用,并掌握过程的选取,及功的正负值,注意本题随着a纸张的越高则小球获得的动能越小,则穿过的可能性越小.因此只有动能大于或等于3J时,才可能穿过.
解答:解:当ab为紧靠着的、且两边固定的两张相同的薄纸,根据动能定理,则有:WG+Wf=0-0.
所以Wf=-WG=-1×10×0.6J=-6J,因此小球穿破两张纸的瞬间损失的机械能为6J.
a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则当小球的动能达到3J时,才能穿破纸张.
设释放点距a纸距离为L,根据动能定理,则有:mgL≥3J,解得:L≥30cm.因此a纸距离b纸不超过30cm.
故答案为:6;30.
点评:考查动能定理的应用,并掌握过程的选取,及功的正负值,注意本题随着a纸张的越高则小球获得的动能越小,则穿过的可能性越小.因此只有动能大于或等于3J时,才可能穿过.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013?辽宁一模)ab为紧靠着的、且两边固定的两张相同薄纸,如图所示.一个质量为1kg的小球从距纸面高为60cm的地方自由下落,恰能穿破两张纸(即穿过后速度为零).若将a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则a纸距离b纸不超过( )
(2013?辽宁一模)ab为紧靠着的、且两边固定的两张相同薄纸,如图所示.一个质量为1kg的小球从距纸面高为60cm的地方自由下落,恰能穿破两张纸(即穿过后速度为零).若将a纸的位置升高,b纸的位置不变,在相同条件下要使小球仍能穿破两张纸,则a纸距离b纸不超过( )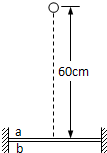 ab为紧靠着的、且两边固定的两张相同的薄纸,如图所示.一个质量为1kg的小球从距纸面高为60cm的地方自由下落,恰能穿破两张纸(即穿过后速度为零),则小球穿破纸的瞬间损失的机械能为
ab为紧靠着的、且两边固定的两张相同的薄纸,如图所示.一个质量为1kg的小球从距纸面高为60cm的地方自由下落,恰能穿破两张纸(即穿过后速度为零),则小球穿破纸的瞬间损失的机械能为