题目内容
【题目】如图所示,A、B是两个质量均为m=1 kg的小球,两球由长L=4 m的轻杆相连组成系统,水平面上的P、Q两点间是一段长度为4.5 m的粗糙平面,其余部分表面光滑,小球与PQ间的动摩擦因数μ=0.2,球A、B分别静止在P点两侧,离P点的距离均为![]() .两球均可视为质点,不计轻杆质量,现对B球施加一水平向右F=4 N的拉力,取g=10 m/s2,求:
.两球均可视为质点,不计轻杆质量,现对B球施加一水平向右F=4 N的拉力,取g=10 m/s2,求:
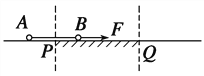
(1)A球经过P点时的速度大小;
(2)若当A球经过P点时立即撤去F,最后A、B球静止,A球静止时与Q点的距离.
【答案】(1)2 m/s(2)3m
【解析】(1)设系统开始运动时加速度为a1,由牛顿第二定律有F-μmg=2ma1
解得a1=1 m/s2
设A球经过P点时速度为v1,则![]() =2a1·
=2a1·![]() 得v1=2 m/s
得v1=2 m/s
(2)设A、B在P、Q间做匀减速运动时加速度大小为a2,则有
2μmg=2ma2
a2=μg=2 m/s2
当A球经过P点时拉力F撤去,但系统将继续滑行,设当B到达Q时滑行的距离为x1,速度为v2,则有x1=xPQ-L=0.5 m
由![]()
解得v2=![]() m/s
m/s
因为v2>0,故知B球将通过Q点,做匀减速直线运动,此时加速度大小为a3.
则有μmg=2ma3
a3=1 m/s2
设系统继续滑行x2后静止,则有
0-![]() =-2a3x2
=-2a3x2
可得x2=1 m
即A球静止时与Q点的距离Δx=L-x2=3 m

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目