题目内容
【题目】如图所示,一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场,在ad边中点O,方向垂直磁场向里射入一速度方向跟ad边夹角![]() 、大小为v0(未知量)的带正电粒子,己知粒子质量为m,电量为q,ad边长为L,ab边足够长,粒子重力不计,求:
、大小为v0(未知量)的带正电粒子,己知粒子质量为m,电量为q,ad边长为L,ab边足够长,粒子重力不计,求:

(1)若粒子恰好不能从磁场下边界射出,求粒子的入射速度大小v01;
(2)若粒子能从ad边射出,求粒子的入射速度大小v02的取值范围。
【答案】(1)![]() (2)v20≤
(2)v20≤![]()
【解析】
(1)粒子在磁场中做匀速圆周运动,作出粒子运动轨迹,求出粒子轨道半径,然后应用牛顿第二定律求出粒子的速度.(2)若粒子能从ad边射出,则讨论临界条件是粒子的轨迹与ab相切,由几何关系找到半径,然后求解能从ad边射出时速度的最大值.
(1)粒子恰好不能从磁场下边界射出时,运动轨迹恰好与dc相切,粒子运动轨迹如图所示: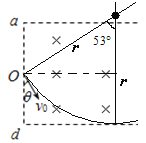
由几何知识得:r-rcos53°=![]() L,
L,
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qv10B=m![]() ,
,
解得:v10=![]() ;
;
(2)当粒子的运动轨迹与ab相切时粒子恰好从ad边射出,此时r′+r′sin370=![]() L
L
解得![]() ;
;
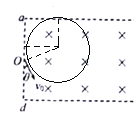
由牛顿第二定律得:qv20B=m![]() ,
,
解得:v20=![]() ;
;
若粒子能从ad边射出,粒子的入射速度大小v02的取值范围为:v20≤![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目