题目内容
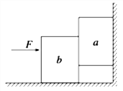
【题目】如图所示,有一个可视为质点的质量为m=1kg的小物块,从光滑平台上的A点以v0=3m/s的初速度水平抛出,到达C点时,恰好沿C点的切线方向进入固定在水平地面上的光滑圆弧轨道,最后小物块滑上紧靠轨道末端D点的质量为M=3kg的长木板.已知木板上表面与圆弧轨道末端切线相平,木板下表面与水平地面之间光滑,小物块与长木板间的动摩擦因数μ=0.3,圆弧轨道的半径为R=0.5m,C点和圆弧的圆心连线与竖直方向的夹角θ=53°,不计空气阻力,取重力加速度为g=10m/s2 . 求:
(1)AC两点的高度差;
(2)小物块刚要到达圆弧轨道末端D点时对轨道的压力;
(3)要使小物块不滑出长木板,木板的最小长度.(sin53°=0.8,cos53°=0.6)
【答案】
(1)
解:小物块在C点速度大小为:vC= ![]() =5 m/s,
=5 m/s,
竖直分量:vCy=4 m/s
下落高度:h= ![]() =0.8m
=0.8m
答: AC两点的高度差为0.8m.
(2)
小物块由C到D的过程中,由动能定理得:
mgR(1﹣cos 53°)= ![]()
解得:vD= ![]() m/s
m/s
小球在D点时由牛顿第二定律得:FN﹣mg=m ![]()
代入数据解得:FN=68N
由牛顿第三定律得FN′=FN=68N,方向竖直向下
答:小物块刚要到达圆弧轨道末端D点时对轨道的压力为68N.
(3)
设小物块刚滑到木板左端达到共同速度,大小为v,小物块在木板上滑行的过程中,小物块与长木板的加速度大小分别为:
a1=μg=3 m/s2,a2= ![]() =1 m/s2
=1 m/s2
速度分别为:v=vD﹣a1t,v=a2t
对物块和木板系统,由能量守恒定律得:
μmgL= ![]() mvD2﹣
mvD2﹣ ![]() (m+M) v2
(m+M) v2
解得:L=3.625 m,即木板的长度至少是3.625 m
答:木板的最小长度为3.625m.
【解析】(1)小球从A点抛出做平抛运动,将C点的速度进行分解,求出竖直分速度的大小,从而根据竖直方向上的运动规律求出AC两点的高度差.(2)求出C点的速度,对C到D运用动能定理求出到达D点的速度,根据牛顿第二定律求出支持力的大小,从而得出物块对轨道的压力.(3)当小物块刚好不从长木板滑出时,与木板具有相同的速度,根据牛顿第二定律和运动学公式求出共同的速度,因为摩擦力与相对路程的乘积等于产生的热量,结合能量守恒定律求出木板的长度.
【考点精析】关于本题考查的牛顿第三定律和平抛运动,需要了解牛顿第三运动定律指出了两物体之间的作用是相互的,因而力总是成对出现的,它们总是同时产生,同时消失;作用力和反作用力总是同种性质的力;作用力和反作用力分别作用在两个不同的物体上,各产生其效果,不可叠加;特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动才能得出正确答案.