题目内容
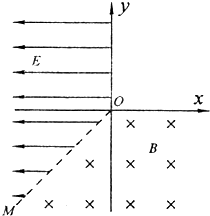 如图所示,在纸面内建立直角坐标系xOy,以第Ⅲ象限内的直线OM(与负x轴成45°角)和正y轴为界,在x<0的区域建立匀强电场,方向水平向左,场强大小E=2V/m;以直线OM和正x轴为界,在y<0的区域建立垂直纸面向里的匀强磁场,磁感应强度B=0.1T.一不计重力的带负电微粒,从坐标原点O沿y轴负方向以v0=2×103m/s的初速度射入磁场.已知微粒的比荷为
如图所示,在纸面内建立直角坐标系xOy,以第Ⅲ象限内的直线OM(与负x轴成45°角)和正y轴为界,在x<0的区域建立匀强电场,方向水平向左,场强大小E=2V/m;以直线OM和正x轴为界,在y<0的区域建立垂直纸面向里的匀强磁场,磁感应强度B=0.1T.一不计重力的带负电微粒,从坐标原点O沿y轴负方向以v0=2×103m/s的初速度射入磁场.已知微粒的比荷为| q |
| m |
(1)粒子经过
| 1 |
| 4 |
(2)粒子在磁场区域运动的总时间;
(3)粒子最终将从电场区域D点离开电场,则D点离O点的距离是多少?
分析:(1)粒子做匀速圆周运动,根据牛顿第二定律,求出运动的半径,从而即可求解;
(2)根据圆周运动的周期公式,可求出在磁场中总时间;
(3)粒子做类平抛运动,将其运动分解,运用运动学公式与牛顿第二定律,即可求解.
(2)根据圆周运动的周期公式,可求出在磁场中总时间;
(3)粒子做类平抛运动,将其运动分解,运用运动学公式与牛顿第二定律,即可求解.
解答: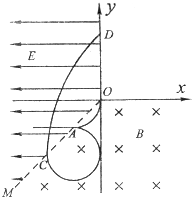 解:(1)微粒带负电,从O点射入磁场,沿顺时针方向做圆周运动,轨迹如图.
解:(1)微粒带负电,从O点射入磁场,沿顺时针方向做圆周运动,轨迹如图.
第一次经过磁场边界上的A点
由qv0B=m
,
得r=
=0.4m,
所以,A点坐标为(-0.4m,-0.4m).
(2)设微粒在磁场中做圆周运动的周期为T,则
t1=tOA+tAC=
+
,
其中T=
代入数据解得:T=1.256×10-3s
所以t=1.26×10-3s.
(3)微粒从C点沿y轴正方向进入电场,做类平抛运动,则
由牛顿第二定律,qE=ma
△x=
a
=2r
△y=v0t1
代入数据解得:△y=8m
y=△y-2r=8-2×0.4m=7.2m
即:离开电磁场时距O点的距离为7.2m.
答:(1)粒子经过
圆弧第一次经过磁场边界时的位置坐标为(-0.4m,-0.4m);
(2)粒子在磁场区域运动的总时间1.26×10-3s;
(3)粒子最终将从电场区域D点离开电场,则D点离O点的距离是7.2m.
 解:(1)微粒带负电,从O点射入磁场,沿顺时针方向做圆周运动,轨迹如图.
解:(1)微粒带负电,从O点射入磁场,沿顺时针方向做圆周运动,轨迹如图.第一次经过磁场边界上的A点
由qv0B=m
| ||
| r |
得r=
| mv0 |
| Bq |
所以,A点坐标为(-0.4m,-0.4m).
(2)设微粒在磁场中做圆周运动的周期为T,则
t1=tOA+tAC=
| T |
| 4 |
| 3T |
| 4 |
其中T=
| 2πm |
| Bq |
代入数据解得:T=1.256×10-3s
所以t=1.26×10-3s.
(3)微粒从C点沿y轴正方向进入电场,做类平抛运动,则
由牛顿第二定律,qE=ma
△x=
| 1 |
| 2 |
| t | 2 1 |
△y=v0t1
代入数据解得:△y=8m
y=△y-2r=8-2×0.4m=7.2m
即:离开电磁场时距O点的距离为7.2m.
答:(1)粒子经过
| 1 |
| 4 |
(2)粒子在磁场区域运动的总时间1.26×10-3s;
(3)粒子最终将从电场区域D点离开电场,则D点离O点的距离是7.2m.
点评:考查牛顿第二定律在匀速圆周运动中、类平抛运动中的应用,并根据运动的合成与分解来解题,紧扣运动的时间相等性.

练习册系列答案
相关题目
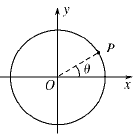
如图所示,平行于纸面有一匀强电场(电场未画出),在纸面内建了一个直角坐标系xOy,以O为圆心,做半径r=2 cm的圆.如果在圆上任取一点P,设OP与x轴正方向的夹角为θ,P点的电势与θ角函数关系满足φP="[8cos(θ-30°)+10]" V.则下列说法正确的是( )
| A.当θ=90°时,P点的电势为10 V |
| B.当θ=330°时,P点的电势与当θ=90°时P点的电势相等 |
| C.该电场强度的方向与x轴负方向成60°角斜向下 |
| D.该圆周上的电势最低点是θ=30°时的P点 |