题目内容
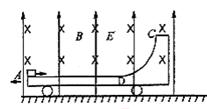
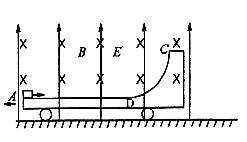
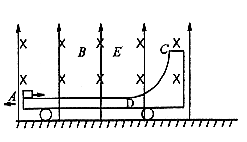
 如图所示,质量为3.0kg的小车以1.0m/s的速度在光滑的水平面上向左运动,车上AD部分是表面粗糙的水平轨道,DC部分是1/4光滑圆弧,整个轨道都是由绝缘材料制成的,小车所在空间内有竖直向上的匀强电场和垂直纸面向里的匀强磁场,电场强度E为40N/C,磁感应强度B为2.0T.现有一质量为1.0kg、带负电且电荷量为1.0×10-2C的滑块以8m/s的水平速度向右冲上小车,当它通过D点时速度为5.0m/s(滑块可视为质点,g取10m/s2),求:(计算结果保留两位有效数字)
如图所示,质量为3.0kg的小车以1.0m/s的速度在光滑的水平面上向左运动,车上AD部分是表面粗糙的水平轨道,DC部分是1/4光滑圆弧,整个轨道都是由绝缘材料制成的,小车所在空间内有竖直向上的匀强电场和垂直纸面向里的匀强磁场,电场强度E为40N/C,磁感应强度B为2.0T.现有一质量为1.0kg、带负电且电荷量为1.0×10-2C的滑块以8m/s的水平速度向右冲上小车,当它通过D点时速度为5.0m/s(滑块可视为质点,g取10m/s2),求:(计算结果保留两位有效数字)(1)滑块从A到D的过程中,小车、滑块组成的系统损失的机械能;
(2)如果圆弧轨道半径为1.0m,求滑块刚过D点时对轨道的压力;
(3)若滑块通过D点时,立即撤去磁场,要使滑块不冲出圆弧轨道,此圆弧的最小半径.
分析:(1)滑块从A到D的过程中,小车、滑块系统水平方向不受外力,水平方向动量守恒,可求出滑块到达D点时车的速度,系统损失的机械能等于系统动能的减小.
(2)滑块通过D时受到重力、支持力、电场力和洛伦兹力,合力提供向心力,写出动力学方程即可求出轨道对滑块的支持力;然后根据牛顿第三定律说明;
(3)要使滑块不冲出圆弧轨道,滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同速度v,根据动量守恒定律和能量的转化与守恒定律求得结果.
(2)滑块通过D时受到重力、支持力、电场力和洛伦兹力,合力提供向心力,写出动力学方程即可求出轨道对滑块的支持力;然后根据牛顿第三定律说明;
(3)要使滑块不冲出圆弧轨道,滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同速度v,根据动量守恒定律和能量的转化与守恒定律求得结果.
解答:解:(1)设滑块运动到D点时的速度为v1,小车在此时的速度为v2′
滑块从A运动到D的过程中系统动量守恒mv0+Mv2=mv1+Mv2′
小车的速度为v2′=0
小车与滑块组成的系统损失的机械能为△E,△E=
m
+
M
-
m
△E=21J
(2)设滑块刚过D点时,受到轨道的支持力为N,N-(mg+qE+qv1B)=
得N=35.5N
滑块对轨道压力N′=N=35.5N
(3)滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同速度v
由动量守恒定律mv1=(m+M)v
v=
m/s
设圆弧轨道的最小半径为Rmin
由能量守恒关系
m
=
(m+M)v2+(mg+qE)Rmin
代人数据解得:Rmin=0.90m
答:(1)小车、滑块组成的系统损失的机械能是21J;
(2)滑块刚过D点时对轨道的压力35.5N;
(3)若滑块通过D点时,立即撤去磁场,要使滑块不冲出圆弧轨道,此圆弧的最小半径为0.90m.
滑块从A运动到D的过程中系统动量守恒mv0+Mv2=mv1+Mv2′
小车的速度为v2′=0
小车与滑块组成的系统损失的机械能为△E,△E=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
△E=21J
(2)设滑块刚过D点时,受到轨道的支持力为N,N-(mg+qE+qv1B)=
m
| ||
| R |
得N=35.5N
滑块对轨道压力N′=N=35.5N
(3)滑块沿圆弧轨道上升到最大高度时,滑块与小车具有共同速度v
由动量守恒定律mv1=(m+M)v
v=
| 5 |
| 4 |
设圆弧轨道的最小半径为Rmin
由能量守恒关系
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
代人数据解得:Rmin=0.90m
答:(1)小车、滑块组成的系统损失的机械能是21J;
(2)滑块刚过D点时对轨道的压力35.5N;
(3)若滑块通过D点时,立即撤去磁场,要使滑块不冲出圆弧轨道,此圆弧的最小半径为0.90m.
点评:本题是系统动量守恒和能量守恒的类型,寻找解题规律是关键.容易出错的地方,是不认真分析滑块运动过程,认为滑块刚到达D时车的速度就最大.

练习册系列答案
相关题目