题目内容
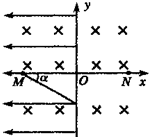
 如图所示,地面附近的坐标系xoy在竖直平面内,空气有沿水平方向垂直于纸面向里、磁感应强度大小为B的匀强磁场,在x<0的空间内还有沿x轴负方向、场强大小为E的匀强电场.一个带正电的油滴经图中x轴上的M点,沿与水平方向成a=30°角斜向下的直线运动,进入x>0的区域.要使油滴进入x>0的区域后能在竖直平面内做匀速圆周运动,需在x>0区域加一个匀强电场.若带电油滴做圆周运动通过x轴上的N点,且MO=ON,重力加速度为g,求:
如图所示,地面附近的坐标系xoy在竖直平面内,空气有沿水平方向垂直于纸面向里、磁感应强度大小为B的匀强磁场,在x<0的空间内还有沿x轴负方向、场强大小为E的匀强电场.一个带正电的油滴经图中x轴上的M点,沿与水平方向成a=30°角斜向下的直线运动,进入x>0的区域.要使油滴进入x>0的区域后能在竖直平面内做匀速圆周运动,需在x>0区域加一个匀强电场.若带电油滴做圆周运动通过x轴上的N点,且MO=ON,重力加速度为g,求:(1)油滴运动的速度大小;
(2)在x>0区域内所加电场的场强大小及方向;
(3)油滴从M点到N点所用的时间.
分析:(1)油滴沿着直线MP做匀速运动,合力为零,作出油滴的受力示意图,根据平衡条件和洛伦兹力公式列式,即可求得速率v.
(2)在x>0的区域,油滴要做匀速圆周运动,其所受的电场力必与重力平衡,则可由平衡条件列式求得场强.
(3)分段求时间,匀速直线运动过程,根据位移和速率求解;匀速圆周运动过程,画出轨迹,根据轨迹的圆心角求时间.
(2)在x>0的区域,油滴要做匀速圆周运动,其所受的电场力必与重力平衡,则可由平衡条件列式求得场强.
(3)分段求时间,匀速直线运动过程,根据位移和速率求解;匀速圆周运动过程,画出轨迹,根据轨迹的圆心角求时间.
解答:解:(1)带电油滴在x<0区域内受重力mg,电场力qE和洛仑兹力f,油滴沿直线运动,重力和电场力为恒力,则与运动方向垂直的洛仑兹力f的大小一定不能变化,因此油滴一定做匀速直线运动.
由平衡条件可知qvB=
①
mg=qEcotα②
由①②两式代人数据得v=
③
=
④
(2)因油滴进入x>0区域后做匀速圆周运动,
所受电场力qE'与重力等大反向,
即qE'=mg⑤
由④⑤得E′=
E⑥方向竖直向上.
(3)油滴从P点进入x>0区域,然后做匀速圆周运动,其轨迹所对应的圆心角为120°,油滴从P到N的时间
 t2=
t2=
=
⑦
由④⑦得:t2=
⑧
由几何关系可知:图中MP=
R,油滴从M到P的时间t1=
⑨
又R=
⑩
又④⑨⑩得t 1=
从M到N的总时间t=t 1+t2=(3+
)
答:(1)油滴运动的速度是v=
;
(2)在x>0区域内所加电场的场强大小 E′=
E,方向竖直向上;
(3)油滴从M点到N点所用的时间t=(3+
)
.
由平衡条件可知qvB=
| qE |
| sinα |
mg=qEcotα②
由①②两式代人数据得v=
| 2E |
| B |
| m |
| q |
| ||
| g |
(2)因油滴进入x>0区域后做匀速圆周运动,
所受电场力qE'与重力等大反向,
即qE'=mg⑤
由④⑤得E′=
| 3 |
(3)油滴从P点进入x>0区域,然后做匀速圆周运动,其轨迹所对应的圆心角为120°,油滴从P到N的时间
 t2=
t2=| T |
| 3 |
| 2πm |
| 3qB |
由④⑦得:t2=
2
| ||
| 3Bg |
由几何关系可知:图中MP=
| 3 |
| ||
| v |
又R=
| mv |
| Bg |
又④⑨⑩得t 1=
| 3E |
| Bg |
从M到N的总时间t=t 1+t2=(3+
2π
| ||
| 3 |
| E |
| Bg |
答:(1)油滴运动的速度是v=
| 2E |
| B |
(2)在x>0区域内所加电场的场强大小 E′=
| 3 |
(3)油滴从M点到N点所用的时间t=(3+
2π
| ||
| 3 |
| E |
| Bg |
点评:本题是带电体在复合场中运动的类型,分析受力情况和运动情况是基础,小球做匀速圆周运动时,画出轨迹,由几何知识确定圆心角是求解运动时间的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目