题目内容
汤姆逊用来测定电子的比荷实验装置如下:真空管内的阴极C发出电子,(不计初速,重力和电子间相互作用),经过A、B间的电场加速后,穿过A、B的中心小孔沿中心轴O′O的方向进入到两块水平正对的长度为L的平行极板D和E间的区域,当极板间不加偏转电压时,电子束打在荧光屏的中心O′点,形成一个亮点;若在D、E间加上方向向下、场强为E的匀强电场,电子将向上偏转;如果再利用通电线圈在D、E电场区加上一垂直纸面的匀强磁场(图中未画出),调节磁场的强弱,当磁感应强度的大小为B时,荧光斑恰好回到荧光屏中心.接着再去掉电场,电子向下偏转,偏转角为φ.如图所示,求:
(1)在图中画出磁场B的方向;
(2)根据L、E、B和φ,推导电子的比荷的表达式.

(1)在图中画出磁场B的方向;
(2)根据L、E、B和φ,推导电子的比荷的表达式.

分析:(1)当电子受到电场力与洛伦兹力平衡时,做匀速直线运动,再由竖直向下的匀强电场,根据左手定则可确定磁场方向;
(2)当电子受到电场力与洛伦兹力平衡时,因此由电压、磁感应强度可求出运动速度.电子在磁场中做匀速圆周运动,则画出圆轨道,找出半径与已知长度的关系,然后由洛伦兹力提供向心力,来推导电子的比荷的表达式.
(2)当电子受到电场力与洛伦兹力平衡时,因此由电压、磁感应强度可求出运动速度.电子在磁场中做匀速圆周运动,则画出圆轨道,找出半径与已知长度的关系,然后由洛伦兹力提供向心力,来推导电子的比荷的表达式.
解答:解:粒子在磁场中做匀速圆周运动,如图所示,

则有:L=
?cosθ
解之得:
=
=
又
=Rsinθ=Rsin
所以
=R
因为2cos
?sin
=sinφ
得:L=Rsinφ
由题意可得:qvB=qE
则有:v=
洛伦兹力提供向心力,则有:qvB=m
=m
综上所得:qB=m
=m
即
=
答:(1)在图中画出磁场B的方向垂直纸面向里;
(2)根据L、E、B和φ,推导电子的比荷的表达式

则有:L=
. |
| AB |
解之得:
. |
| AB |
| L |
| cosθ |
| L | ||
cos
|
又
| ||
| 2 |
| φ |
| 2 |
所以
| L | ||||
2cos
|
因为2cos
| φ |
| 2 |
| φ |
| 2 |
得:L=Rsinφ
由题意可得:qvB=qE
则有:v=
| E |
| B |
洛伦兹力提供向心力,则有:qvB=m
| v2 |
| R |
| v2 | ||
|
综上所得:qB=m
| v | ||
|
| Esinφ |
| BL |
即
| q |
| m |
| Esinφ |
| B2L |
答:(1)在图中画出磁场B的方向垂直纸面向里;
(2)根据L、E、B和φ,推导电子的比荷的表达式
| Esinφ |
| B2L |
点评:考查带电粒子在匀强磁场中做匀速圆周运动,(画轨迹、定圆心、求半径),运用牛顿第二定律来推导.
若粒子做平抛运动,则可运用平抛运动处理规律:将运动分解成相互垂直的两方向运动,因此将一个复杂的曲线运动分解成两个简单的直线运动,并用运动学公式来求解.
若粒子做平抛运动,则可运用平抛运动处理规律:将运动分解成相互垂直的两方向运动,因此将一个复杂的曲线运动分解成两个简单的直线运动,并用运动学公式来求解.

练习册系列答案
相关题目

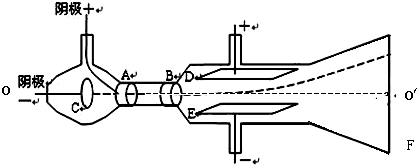

 过A、B间的电场加速后,穿过A、B的中心小孔沿中心轴O/O的方向进入到两块水平正对的长度为L的平行极板D和E间的区域,当极板间不加偏转电压时,电子束打在荧光屏的中心O'点,形成一个亮点;若在D、E间加上方向向下、场强为E的匀强电场,电子将向上偏转;如果再利用通电线圈在D、E电场区加上一垂
过A、B间的电场加速后,穿过A、B的中心小孔沿中心轴O/O的方向进入到两块水平正对的长度为L的平行极板D和E间的区域,当极板间不加偏转电压时,电子束打在荧光屏的中心O'点,形成一个亮点;若在D、E间加上方向向下、场强为E的匀强电场,电子将向上偏转;如果再利用通电线圈在D、E电场区加上一垂 直纸面的匀强磁场(图中未画出),调节磁场的强弱,当磁感应强度的大小为B时,荧光斑恰好回到荧光屏中心。接着再去掉电场,电子向下偏转,偏转角为φ。如图所示,求(1)在图中画出磁场B的方向 (2)根据L、E、B和φ,推导电子的比荷的表达式。
直纸面的匀强磁场(图中未画出),调节磁场的强弱,当磁感应强度的大小为B时,荧光斑恰好回到荧光屏中心。接着再去掉电场,电子向下偏转,偏转角为φ。如图所示,求(1)在图中画出磁场B的方向 (2)根据L、E、B和φ,推导电子的比荷的表达式。