题目内容
1.玻璃生产线上,宽为10m的成型玻璃以3m/s的速度连续不断地在平直的轨道上前进,在切割工序处,金刚石切割刀以5m/s的速度切割玻璃,且每次割下的玻璃板都成规定尺寸的矩形.(sin37°=0.6,cos37°=0.8)求:(1)金刚刀切割的速度方向与玻璃板前进方向的夹角θ;
(2)切割一次玻璃板的时间.
分析 割刀实际参与两个分运动,即沿玻璃的运动和垂直玻璃方向的运动.根据运动的合成确定运动的轨迹以及合速度.根据分运动与合运动具有等时性,求出完成一次切割所需的时间.
解答 解:割刀实际参与两个分运动,即沿玻璃的运动和垂直玻璃方向的运动,所以金钢钻割刀应与垂直玻璃方向一定的角度运动进行切割,
根据平行四边形定则知,割刀运动的实际速度为:v=$\sqrt{{v}_{1}^{2}-{v}_{2}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$m/s=4m/s,
切割的时间为:t=$\frac{d}{v}$=$\frac{10}{4}$s=2.5s.
设金刚钻割刀的轨道与玻璃板速度方向的夹角为θ,则cosθ=$\frac{{v}_{2}}{{v}_{1}}$=0.6,即:θ=53°.
答:(1)金刚钻割刀的轨道与玻璃板速度方向夹角为53°,
(2)切割一次玻璃板的时间为2.5s.
点评 解决本题的关键知道割刀实际参与两个分运动,即沿玻璃的运动和垂直玻璃方向的运动.知道合运动与分运动具有等时性,以及会用平行四边形定则求合速度.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.下列物理量是矢量的有( )
| A. | 电场强度 | B. | 电势差 | C. | 电势能 | D. | 电量 |
16.下列说法正确的是( )
| A. | 任何形状规则的物体,它的重心均与其几何中心重合 | |
| B. | 质量大的物体重力大,做自由落体运动时重力加速度大 | |
| C. | 滑动摩擦力总是与物体的运动方向相反 | |
| D. | 两个接触面之间有摩擦力则一定有弹力,且摩擦力方向一定与弹力方向垂直 |
6.关于曲线运动下列说法中正确的是( )
| A. | 物体做曲线运动时,合外力与速度方向可能相同 | |
| B. | 物体做曲线运动时,所受的合外力一定不为零 | |
| C. | 做匀速圆周运动的物体,速度不随时间改变 | |
| D. | 做平抛运动的物体,速度和加速度都随时间改变 |
13.一个电池组的电动势为E,内阻为r,用它给一个线圈电阻为R的直流电动机供电,当电动机正常工作时,通过电动机的电流为I,电动机两端的电压为U,经t(s)后,则( )
| A. | 电源在内外电路做的功为IUt | B. | 电池消耗的化学能为IEt | ||
| C. | 电动机输出的机械能为IEt-I2rt | D. | 电池组的效率$\frac{U-Ir}{E}$ |
10.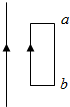 在同一竖直平面内有竖直放置的长直导线与矩形线圈(ab边与直导线平行),它们通有如图所示的电流,则ab边受到的安培力方向为( )
在同一竖直平面内有竖直放置的长直导线与矩形线圈(ab边与直导线平行),它们通有如图所示的电流,则ab边受到的安培力方向为( )
 在同一竖直平面内有竖直放置的长直导线与矩形线圈(ab边与直导线平行),它们通有如图所示的电流,则ab边受到的安培力方向为( )
在同一竖直平面内有竖直放置的长直导线与矩形线圈(ab边与直导线平行),它们通有如图所示的电流,则ab边受到的安培力方向为( )| A. | 水平向左 | B. | 水平向右 | C. | 垂直纸面向里 | D. | 垂直纸面向外 |
13. 如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN.重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )
如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN.重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )
 如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN.重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )
如图所示,一质量为m的质点在半径为R的半球形容器中(容器固定)由静止开始自边缘上的A点滑下,到达最低点B时,它对容器的正压力为FN.重力加速度为g,则质点自A滑到B的过程中,摩擦力对其所做的功为( )| A. | $\frac{1}{2}$R(FN-3mg) | B. | $\frac{1}{2}$R(2mg-FN) | C. | $\frac{1}{2}$R(FN-mg) | D. | $\frac{1}{2}$R(FN-2mg) |
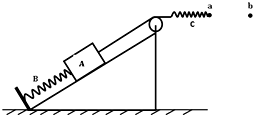 如图所示,劲度系数为k1的轻质弹簧B的两端分别与固定斜面上的挡板及物体A相连,A的质量为m,光滑斜面倾角为θ.用轻绳跨过定滑轮将物体A与另一根劲度系数为k2的轻质弹簧C连接.当弹簧C处在水平位置且未发生形变时,其右端点位于a位置.现将弹簧C的右端点用力沿水平方向缓慢拉到b位置时,弹簧B对物体A的拉力大小恰好等于A的重力.求:
如图所示,劲度系数为k1的轻质弹簧B的两端分别与固定斜面上的挡板及物体A相连,A的质量为m,光滑斜面倾角为θ.用轻绳跨过定滑轮将物体A与另一根劲度系数为k2的轻质弹簧C连接.当弹簧C处在水平位置且未发生形变时,其右端点位于a位置.现将弹簧C的右端点用力沿水平方向缓慢拉到b位置时,弹簧B对物体A的拉力大小恰好等于A的重力.求: