Question

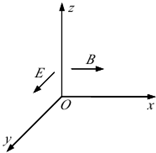
如图所示，某一真空空间内充满着相互垂直的场强为E的匀强电场和磁感应强度为B的匀强磁场，且电场和磁场根据需要可同时存在或单独存在．在此空间中建立Oxyz空间直角坐标系，且xOy位于水平面，
（1）若电场和磁场同时存在，且B和E的方向分别与x轴和y轴正方向相同时，有一电量为+q的带电粒子（重力不计）由坐标原点O沿z轴正方向进入该区域后做匀速直线运动，则该粒子运动速度v为多大？
（2）若有一电量为+q的带电粒子（重力不计）由坐标原点O沿z轴正方向以（1）问中的速度v进入该区域后，仅存在电场，且E的方向沿y轴正方向，当粒子运动方向与z轴正方向的夹角满足tan

3

4

时，撤去电场．经过一段时间后仅加上磁场，且B的方向为x轴的负方向，粒子在以后的运动中正好能与 y 轴相切．问粒子在无电、磁场时的运动时间为仅受电场力作用时间的多少倍？
（3）若电场和磁场同时存在，且B和E的方向分别与x轴和y轴正方向相同时，有一质量为m、带电量为+q的带电小球在yOz平面内做匀速率运动，试判断该小球的运动性质并计算其运动速率．

Answer 1

分析：（1）重力不计，粒子进入场区做匀速直线运动时，受到的洛伦兹力与电场力平衡，由平衡条件列式可求得速度v；
（2）设电场力作用时间为t₁，无电、磁场时的运动时间为t₂．有电场时，粒子做类平抛运动，据题意，粒子运动方向与z轴正方向的夹角满足tan

3

4

时撤去电场，由速度的分解求得粒子沿y轴和z轴两个方向分速度之比

vy

vz

．粒子沿z轴方向做匀速直线运动，AO在z轴上的分位移为 z=v（t₁+t₂），又根据几何关系得：z=R+Rsinθ=1.6R，而粒子圆周运动的半径R=

mv

qB

，联立即可解得时间之比．
（3）小球做匀速直线运动，根据平衡条件列式求速率．

解答：解：（1）由题，粒子进入场区做匀速直线运动时，受到的洛伦兹力与电场力平衡，则有 qE=qvB
解得，v=

E

B

（2）画出粒子在yOz平面内的轨迹如图所示．设电场力作用时间为t₁，无电、磁场时的运动时间为t₂．
当粒子在电场中运动方向与z轴正方向的夹角满足tan

3

4

时，则有
 

vy

vz

=

qE m t1

v

=

3

4

解得，t₁=

3mv

4qE

=

3m

4qB

AO在z轴上的分位移为 z=v（t₁+t₂） ①
由图中几何关系得
   AO在z轴上的分位移为 z=R+Rsinθ=1.6R=

1.6mv合

qB

=

1.6mv

qBcosθ

=

2mv

qB

 ②
由①、②得：t₁+t₂=

2m

qB

，t₂=

5m

4qB

，
所以

t2

t1

=

5

3

（3）小球做匀速直线运动，则

(mg)2+(qE)2

=qvB
解得，v=

(mg)2+(qE)2

qB

答：
（1）粒子运动速度v为

E

B

．
（2）粒子在无电、磁场时的运动时间为仅受电场力作用时间的

5

3

倍？
（3）小球的运动性质是匀速直线运动，其运动速率为

(mg)2+(qE)2

qB

．

点评：本题是带电粒子在复合场中运动的类型，分析粒子的受力情况和运动情况是关键，再运用力学的方法进行处理．