题目内容
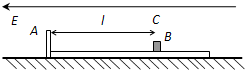 (2007?岳阳县模拟)如图所示,光滑水平面上放有用绝缘材料制成的“L”型滑板,其质量为M,平面部分的上表面光滑且足够长.在距滑板的A端为l的B处放置一个质量为m、带电量为q的小物体C(可看成是质点),在水平的匀强电场作用下,由静止开始运动.已知:M=3m,电场的场强为E.假设物体C在运动中及与滑板A端相碰时不损失电量.
(2007?岳阳县模拟)如图所示,光滑水平面上放有用绝缘材料制成的“L”型滑板,其质量为M,平面部分的上表面光滑且足够长.在距滑板的A端为l的B处放置一个质量为m、带电量为q的小物体C(可看成是质点),在水平的匀强电场作用下,由静止开始运动.已知:M=3m,电场的场强为E.假设物体C在运动中及与滑板A端相碰时不损失电量.(1)求物体C第一次与滑板A端相碰前瞬间的速度大小.
(2)若物体C与滑板A端相碰的时间极短,而且碰后弹回的速度大小是碰前速度大小的
| 1 | 5 |
(3)求小物体C从开始运动到与滑板A第二次碰撞这段时间内,电场力对小物体C做的功.
分析:(1)物体C在电场力作用下做匀加速运动,电场力做功qEl,由动能定理求解C第一次与滑板A端相碰前瞬间的速度大小;
(2)小物体C与滑板碰撞过程中系统合外力为零,由动量守恒定律求出滑板被碰后的速度大小;
(3)分析碰撞后两物体的运动过程;小物体C与滑板碰撞后,滑板向左作做匀速运动;小物体C先向右做匀减速运动,然后向左做匀加速运动,直至与滑板第二次相碰.由于滑块的加速度一定,可以把与滑板碰撞后小物体C看作一种匀减速运动处理.小物体C与滑板从第一次碰后到第二次碰时位移相等.根据牛顿第二定律求出滑块的加速度,由位移公式列出C的位移表达式,结合两者位移相等,求出第一次碰后到第二次碰前的时间.即可求出这段时间内滑板的位移,等于这段时间内C的位移,再求出电场力做功.
(2)小物体C与滑板碰撞过程中系统合外力为零,由动量守恒定律求出滑板被碰后的速度大小;
(3)分析碰撞后两物体的运动过程;小物体C与滑板碰撞后,滑板向左作做匀速运动;小物体C先向右做匀减速运动,然后向左做匀加速运动,直至与滑板第二次相碰.由于滑块的加速度一定,可以把与滑板碰撞后小物体C看作一种匀减速运动处理.小物体C与滑板从第一次碰后到第二次碰时位移相等.根据牛顿第二定律求出滑块的加速度,由位移公式列出C的位移表达式,结合两者位移相等,求出第一次碰后到第二次碰前的时间.即可求出这段时间内滑板的位移,等于这段时间内C的位移,再求出电场力做功.
解答:解:
(1)设物体C在电场力作用下第一次与滑板的A段碰撞时的速度为v1,由动能定理得:
qEl=
mv12 解得:v1=
(2)小物体C与滑板碰撞过程中动量守恒,设滑板碰撞后的速度为v2,由动量守恒定律得
mv1=Mv2-m
v1
解得:v2=
v1=
(3)小物体C与滑板碰撞后,滑板向左作以速度v2做匀速运动;小物体C以
v1的速度先向右做匀减速运动,然后向左做匀加速运动,直至与滑板第二次相碰,设第一次碰后到第二次碰前的时间为t,小物体C在两次碰撞之间的位移为s,根据题意可知,小物体加速度为
a=
小物体C与滑板从第一次碰后到第二次碰时位移相等,即
v2t=-
v1t+
at2 解得:t=
两次相碰之间滑板走的距离s=v2t=
l
设小物体C从开始运动到与滑板A第二次碰撞这段过程电场力对小物体做功为W,则:W=qE(l+s)
解得:W=
qEl
答:(1)物体C第一次与滑板A端相碰前瞬间的速度大小是
.
(2)滑板被碰后的速度大小是
.
(3)电场力对小物体C做的功W=
qEl.
(1)设物体C在电场力作用下第一次与滑板的A段碰撞时的速度为v1,由动能定理得:
qEl=
| 1 |
| 2 |
|
(2)小物体C与滑板碰撞过程中动量守恒,设滑板碰撞后的速度为v2,由动量守恒定律得
mv1=Mv2-m
| 1 |
| 5 |
解得:v2=
| 2 |
| 5 |
| 2 |
| 5 |
|
(3)小物体C与滑板碰撞后,滑板向左作以速度v2做匀速运动;小物体C以
| 1 |
| 5 |
a=
| qE |
| m |
小物体C与滑板从第一次碰后到第二次碰时位移相等,即
v2t=-
| 1 |
| 5 |
| 1 |
| 2 |
| 6 |
| 5 |
|
两次相碰之间滑板走的距离s=v2t=
| 24 |
| 25 |
设小物体C从开始运动到与滑板A第二次碰撞这段过程电场力对小物体做功为W,则:W=qE(l+s)
解得:W=
| 49 |
| 25 |
答:(1)物体C第一次与滑板A端相碰前瞬间的速度大小是
|
(2)滑板被碰后的速度大小是
| 2 |
| 5 |
|
(3)电场力对小物体C做的功W=
| 49 |
| 25 |
点评:本题前两问是常规题,过程与规律都比较简单.难点在第(3)问,关键在于分析物体的运动过程,抓住两物体位移的关系.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
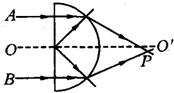 (2007?岳阳县模拟)如图所示,OO′是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于OO′轴等距且平行的两束不同单色细光束,从玻璃射出后相交于OO′下方的P点,由此可以得出的结论是( )
(2007?岳阳县模拟)如图所示,OO′是半圆柱形玻璃体的对称面和纸面的交线,A、B是关于OO′轴等距且平行的两束不同单色细光束,从玻璃射出后相交于OO′下方的P点,由此可以得出的结论是( )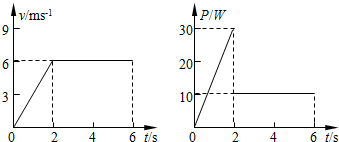 (2007?岳阳县模拟)一放在水平地面上的物体,受到水平拉力作用,在0-6s内其速度-时间图象和力F的功率-时间图象如图所示,则物体的质量为( )(取g=10m/s2)
(2007?岳阳县模拟)一放在水平地面上的物体,受到水平拉力作用,在0-6s内其速度-时间图象和力F的功率-时间图象如图所示,则物体的质量为( )(取g=10m/s2) (2007?岳阳县模拟)电动势为E、内阻为r的电池与固定电阻R0、可变电阻R串联,如图所示,设R0=r,Rab=2r,当变阻器的滑动片自a端向b端滑动时,下列物理量中随之增大的是( )
(2007?岳阳县模拟)电动势为E、内阻为r的电池与固定电阻R0、可变电阻R串联,如图所示,设R0=r,Rab=2r,当变阻器的滑动片自a端向b端滑动时,下列物理量中随之增大的是( )