题目内容
在光滑水平面上有一静止的物体,现以水平恒力F甲推这一物体,作用一段时间后,换成相反方向的水平恒力F乙推这一物体,当恒力F乙作用时间与恒力F甲作用时间相同时,物体恰好回到原处,此时物体的动能为24J,则在整个过程中,恒力F甲做的功等于
6
6
J,恒力F乙做的功等于18
18
J.分析:推力F甲作用时,物体匀加速运动;推力F乙作用时,物体先减速运动,速度减至零后反向加速运动,整个过程加速度不变,可看成一种匀变速运动.
设第一个过程加速运动的末速度为v甲,第二个过程匀变速运动的末速度为v乙,根据平均速度公式可以求出v甲与v乙的关系;然后可根据动能定理求出恒力F甲、F乙做的功.
设第一个过程加速运动的末速度为v甲,第二个过程匀变速运动的末速度为v乙,根据平均速度公式可以求出v甲与v乙的关系;然后可根据动能定理求出恒力F甲、F乙做的功.
解答:解:设第一个物体加速运动的末速度为v甲,第二个物体匀变速运动的末速度为v乙,由于两个运动过程的位移大小相等、方向相反,又由于恒力F乙作用的时间与恒力F甲作用的时间相等,根据平均速度公式有:
t=-
t
解得:v乙=-2v甲
根据动能定理,加速过程
W甲=
mv
W乙=
mv
-
mv
联立以上三式得:
=
可知W甲+W乙=24J,
则W甲=6J、W乙=18J
故答案为:6,18
| 0+v甲 |
| 2 |
| v甲+v乙 |
| 2 |
解得:v乙=-2v甲
根据动能定理,加速过程
W甲=
| 1 |
| 2 |
2 甲 |
W乙=
| 1 |
| 2 |
2 乙 |
| 1 |
| 2 |
2 甲 |
联立以上三式得:
| W甲 |
| W乙 |
| 1 |
| 3 |
可知W甲+W乙=24J,
则W甲=6J、W乙=18J
故答案为:6,18
点评:本题关键在于选用平均速度公式求解出加速过程的末速度和匀变速过程的末速度,然后根据动能定理列式求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
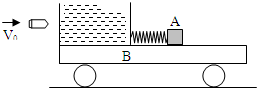 如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99kg.车上静置一物体A,其质量为M2=2.00kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01kg的子弹以水平速度v0=400m/s打入砂箱且静止在砂箱中,求:
如图所示,光滑水平面上有一静止小车B,左端固定一砂箱,砂箱的右端连接一水平轻弹簧,小车与砂箱的总质量为M1=1.99kg.车上静置一物体A,其质量为M2=2.00kg.此时弹簧呈自然长度,物体A的左端的车面是光滑的,而物体A右端的车面与物体间的动摩擦因数为μ=0.2.现有一质量为m=0.01kg的子弹以水平速度v0=400m/s打入砂箱且静止在砂箱中,求:

