题目内容
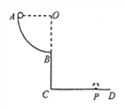
【题目】如图所示，绝缘的1 圆弧轨道AB圆心为O，半径为R；CD为水平面，OC竖直，B为OC的中点。整个空间存在竖直向上的匀强电场，电场强度大小为E。将质量为m、电荷量为+q的小球从A点由静止释放，小球沿轨道运动，通过B点后落到水平面上P点，测得CP=
R。已知重力加速度为g，求：
⑴小球通过B点时对轨道压力的大小；
⑵小球在圆弧轨道上克服阻力做的功。
【答案】(1) 
(2) 
【解析】（1）设小球通过B点时速度为v，小球由B到P的过程中做类平抛运动，加速度为a，由牛顿第二定律及运动学公式得：
小球通过B点时，轨道对小球的支持力为FN，由牛顿第二定律得：
小球通过B点时对轨道的压力为
，根据牛顿第三定律：
FN=
联立解得： 
=2mg-2Eq
（2）小球在圆弧轨道上克服阻力做的功为W，根据动能定理：
解得： 
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
