题目内容
(10分)在“探究单摆摆长与周期关系”的实验中,某同学的主要操作步骤如下:
A.取一根符合实验要求的摆线,下端系一金属小球,上端固定在O点;
B.在小球静止悬挂时测量出O点到小球球心的距离l;
C.拉动小球使细线偏离竖直方向一个不大的角度(约为5°),然后由静止释放小球;
D.用秒表记录小球完成n次全振动所用的时间t。
①用所测物理量的符号表示重力加速度的测量值,其表达式为g= ;
②若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能是
(选填下列选项前的序号)
A、测量摆长时,把摆线的长度当成了摆长
B、摆线上端未牢固地固定于O点,振动中出现松动,使摆线越摆越长
C、测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=t/n求得周期
D、摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后,为了减小实验误差,他决定用图象法处理数据,并通过改变摆长,测得了多组摆长l和对应的周期T,并用这些数据作出T2-l图象如图甲所示。若图线的斜率为k,则重力加速度的测量值g= 。

④这位同学查阅资料得知,单摆在最大摆角q 较大时周期公式可近似表述为 。为了用图象法验证单摆周期T和最大摆角q 的关系,他测出摆长为l的同一单摆在不同最大摆角q 时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
。为了用图象法验证单摆周期T和最大摆角q 的关系,他测出摆长为l的同一单摆在不同最大摆角q 时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
①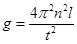 ………(2分);
②C………(2分);③
………(2分);
②C………(2分);③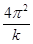 ………(2分);
………(2分);
④sin2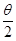 ……(2分,说明:在sin2
……(2分,说明:在sin2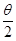 前面加任意符合图象意义的常数均可得分),
前面加任意符合图象意义的常数均可得分),
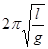 …………(2分)说明:第④问,若第一空:-cosθ,第二空:
…………(2分)说明:第④问,若第一空:-cosθ,第二空: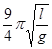 ,则可同样得4分。
,则可同样得4分。
【解析】本题考查的是“探究单摆摆长与周期关系”的实验问题。小球完成n次全振动所用的时间t,则周期为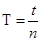 ,由单摆周期公式
,由单摆周期公式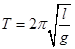 得
得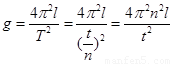 ;若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=t/n求得周期;由T2-l图像可知:
;若测得的重力加速度数值大于当地的重力加速度的实际值,造成这一情况的原因可能测量周期时,误将摆球(n-1)次全振动的时间t记为了n次全振动的时间,并由计算式T=t/n求得周期;由T2-l图像可知: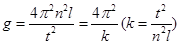 ;图乙中的纵轴表示的是
;图乙中的纵轴表示的是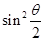 ,图线延长后与横轴交点的横坐标为单摆的周期。
,图线延长后与横轴交点的横坐标为单摆的周期。

在“用单摆测定重力加速度”的实验中:
(1)在测定单摆摆长时,下列操作正确的是__________。
| A.装好单摆,抓住摆球,用力拉紧,测出摆线的悬点到摆球球心之间的距离 |
| B.让单摆自由下垂,测出摆线长度再加摆球直径 |
| C.取下摆线,测出摆线长度后再加上摆球半径 |
| D.测出小球直径,把单摆固定后,让小球自然下垂,用刻度尺量出摆线的长度,再加上小球半径 |
 =__________。
=__________。
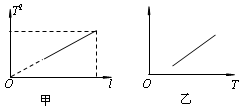
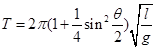 。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。
。为了用图象法验证单摆周期T和最大摆角q的关系,他测出摆长为l的同一单摆在不同最大摆角q时的周期T,并根据实验数据描绘出如图乙所示的图线。根据周期公式可知,图乙中的纵轴表示的是 ,图线延长后与横轴交点的横坐标为 。 =__________。
=__________。