题目内容
11. 如图所示,两绳系一质量为m=0.1kg的小球,上面绳长L=2m,两端都拉直时与轴的夹角分别为30°与45°,问:
如图所示,两绳系一质量为m=0.1kg的小球,上面绳长L=2m,两端都拉直时与轴的夹角分别为30°与45°,问:(1)球的角速度在什么范围内,两绳始终张紧?
(2)当角速度为3rad/s时,上、下两绳拉力分别为多大?
分析 (1)当AC绳拉直但没有力时,BC绳子拉力的水平分力提供向心力,根据牛顿第二定律列式求出此时的角速度,当BC绳拉直但没有力时,AC绳子拉力的水平分力提供向心力,根据牛顿第二定律列式求出角速度,当角速度处于两者之间时,两绳均张紧;
(2)当ω=3rad/s时,AC、BC绳子拉力的水平分力的合力提供向心力,竖直方向分力之和与重力平衡,根据牛顿第二定律列式求解.
解答 解:(1)当AC绳拉直但没有力时,即FT1=0时,由重力和绳BC的拉力FT2的合力提供向心力,根据牛顿第二定律,有:
mgtan45°=m${{ω}_{max}}^{2}r$
其中:r=l•sin30°
解得:ωmax=3.16 rad/s
当FT2恰为零时,根据牛顿第二定律,有:
mgtan30°=m${{ω}_{min}}^{2}r$
解得:ωmin=2.4 rad/s
所以当2.4 rad/s<ω<3.16 rad/s时两绳均张紧.
(2)当ω=3 rad/s时,两绳均处于张紧状态,此时小球受FT1、FT2、mg三力作用,正交分解后可得:
水平方向:FT1sin30°+FT2sin45°=mlsin30°ω2
竖直方向:FT1cos30°+FT2cos45°=mg
代入数据后解得:
FT1=0.27 N
FT2=1.09 N
答:(1)小球的角速度在2.4 rad/s<ω<3.16 rad/s范围内两绳均张紧;
(2)当ω=3rad/s时,AC绳拉力为0.27N,BC绳拉力1.09N.
点评 本题中球做匀速圆周运动,拉力的水平分力提供向心力,关键受力分析后根据牛顿第二定律列式求解,难度适中.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
2.下列说法正确的是( )
| A. | 空气绝对湿度的单位是Pa,空气的相对湿度没有单位 | |
| B. | 可以从单一热源吸收热量并把它全部用来做功,而不引起其他变化 | |
| C. | 利用光学显微镜可以观察到固体分子在液体中做无规则运动 | |
| D. | 饱和蒸气压随温度升高而增大 | |
| E. | 一定质量的理想气体保持体积不变,单位体积内分子数不变,虽然温度升高,单位时间内撞击单位面积上的分子数不变 |
16. 如图所示,水平传送带正以v=2m/s的速度运行,两端的距离为l=8m.把一质量为m=1kg的物体轻轻放到传送带上,物体在传送带的带动下向右运动.物体与传送带间的动摩擦因数μ=0.1,则把这个物体从传送带左端传送到右端的过程中,摩擦力对其做功及摩擦力做功的平均功率分别为( )
如图所示,水平传送带正以v=2m/s的速度运行,两端的距离为l=8m.把一质量为m=1kg的物体轻轻放到传送带上,物体在传送带的带动下向右运动.物体与传送带间的动摩擦因数μ=0.1,则把这个物体从传送带左端传送到右端的过程中,摩擦力对其做功及摩擦力做功的平均功率分别为( )
 如图所示,水平传送带正以v=2m/s的速度运行,两端的距离为l=8m.把一质量为m=1kg的物体轻轻放到传送带上,物体在传送带的带动下向右运动.物体与传送带间的动摩擦因数μ=0.1,则把这个物体从传送带左端传送到右端的过程中,摩擦力对其做功及摩擦力做功的平均功率分别为( )
如图所示,水平传送带正以v=2m/s的速度运行,两端的距离为l=8m.把一质量为m=1kg的物体轻轻放到传送带上,物体在传送带的带动下向右运动.物体与传送带间的动摩擦因数μ=0.1,则把这个物体从传送带左端传送到右端的过程中,摩擦力对其做功及摩擦力做功的平均功率分别为( )| A. | 2 J | B. | 8 J | C. | 1W | D. | 0.4W |
3. 某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化的图象如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em.则下列说法错误的是( )
某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化的图象如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em.则下列说法错误的是( )
 某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化的图象如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em.则下列说法错误的是( )
某兴趣小组自制一小型发电机,使线圈在匀强磁场中绕垂直于磁场方向的固定轴转动,穿过线圈的磁通量Φ随时间t按正弦规律变化的图象如图所示,线圈转动周期为T,线圈产生的电动势的最大值为Em.则下列说法错误的是( )| A. | 在t=$\frac{T}{4}$时,磁场方向与线圈平面平行 | |
| B. | 在t=$\frac{T}{2}$时,线圈中的磁通量变化率最大 | |
| C. | 线圈中电动势的瞬时值e=Emsin($\frac{2πt}{T}$) | |
| D. | 若线圈转速增大为原来的2倍,则线圈中电动势变为原来的4倍 |
20.沿一条直线运动的物体,当物体的加速度逐渐减小时,下列说法正确的是( )
| A. | 物体的速度一定增加的越来越慢 | B. | 物体运动的速度一定减小 | ||
| C. | 物体的速度变化量一定减少 | D. | 物体运动的路程一定增大 |
1.一列简谐横波,某时刻的波形如图甲所示,从该时刻开始计时,波上A质点的振动图象如乙所示,则下列判断正确的是( )
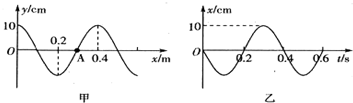

| A. | 该列波沿x轴负方向传播 | |
| B. | 该列波的波速大小为1m/s | |
| C. | 若此波遇到另一列简谐横渡并发生稳定干涉现象,则所遇到的波的频率为0.4Hz | |
| D. | 若该波遇到一障碍物发生了明显的衍射现象,则该障碍物的尺寸和40cm差不多或更小 | |
| E. | 从该时刻起,再经过0.4s的时间,质点A通过的路程为40cm |
 某同学想利用滑块在倾斜气垫导轨上的运动来验证动能定理.如图所示,测量步骤如下:
某同学想利用滑块在倾斜气垫导轨上的运动来验证动能定理.如图所示,测量步骤如下:
 如图所示,在与水平面成θ=30°的平面内放置两条平行、光滑且足够长的金属轨道,其电阻可忽略不计.空间存在着匀强磁场,磁感应强度B=0.20T,方向垂直轨道平面向上.导体棒ab、cd垂直于轨道放置,且与金属轨道接触良好构成闭合回路,每根导体棒的质量m=2.0×10-2kg,回路中每根导体棒电阻r=5.0×10-2Ω,金属轨道宽度l=0.50m.现对导体棒ab施加平行于轨道向上的拉力,使之匀速向上运动.在导体棒ab匀速向上运动过程中,导体棒cd始终能静止在轨道上.g取10m/s2,求:
如图所示,在与水平面成θ=30°的平面内放置两条平行、光滑且足够长的金属轨道,其电阻可忽略不计.空间存在着匀强磁场,磁感应强度B=0.20T,方向垂直轨道平面向上.导体棒ab、cd垂直于轨道放置,且与金属轨道接触良好构成闭合回路,每根导体棒的质量m=2.0×10-2kg,回路中每根导体棒电阻r=5.0×10-2Ω,金属轨道宽度l=0.50m.现对导体棒ab施加平行于轨道向上的拉力,使之匀速向上运动.在导体棒ab匀速向上运动过程中,导体棒cd始终能静止在轨道上.g取10m/s2,求: