Question

如图4-4-22所示，一个长为L、质量为M的长方形木块，静止在光滑水平面上，一个质量为m的物块（可视为质点），以水平初速度v₀从木块的左端滑向右端，设物块与木块间的动摩擦因数为μ，当物块与木块达到相对静止时，物块仍在长木块上，求系统机械能转化成内能的量Q.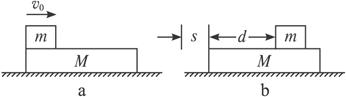

图4-4-22

Answer 1

思路点拨：可先根据动量守恒定律求出m和M的共同速度，再根据动能定理或能量守恒求出转化为内能的量Q.

解析：对物块，滑动摩擦力f做负功，由动能定理得-f(d+s)= mv_t²-mv₀²，即f对物块做负功，使物块动能减少.

对木块，滑动摩擦力f对木块做正功，由动能定理得fs=Mv²-0，即f对木块做正功，使木块动能增加，系统减少的机械能为mv₀²-mv_t²-Mv²=f(d+s)-fs=fd.                 ①

本题中f=μmg，物块与木块相对静止时，v=v_t，则上式可简化为

μmgd=mv₀²-(m+M)v_t²                                                      ②

又以物块、木块为系统，系统在水平方向不受外力，动量守恒，则mv₀=(m+M)v_t        ③

联立②③得：d=，故系统机械能转化为内能的量为

Q=fd=μmg·=.

答案：