题目内容
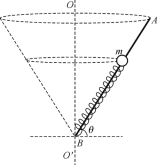
【题目】如图所示，半径R = 0．8m的光滑绝缘导轨固定于竖直平面内，加上某一水平方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动，它的电量q＝1．00×10－7C。圆心O与A点的连线与竖直成一角度θ，在A点时小球对轨道的压力N =1．2N，此时小球的动能最大。若小球的最大动能比最小动能多0．32J，且小球能够到达轨道上的任意一点（不计空气阻力，g取10m/s2）。
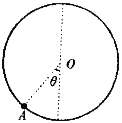
求：（1）小球受到重力和电场力的合力；
（2）小球的最小动能；
（3）现小球在动能最小的位置突然撤去轨道，并保持其他量都不变，若小球在0．4s后的动能与它在A点时的动能相等，求小球的质量和电场强度。
【答案】（1）
；（2）
；（3）
，
。
【解析】
试题分析：（1）小球在电场和重力场的复合场中运动，在A点动能最大，重力和电场力的合力的方向由O指向A，在AO延长线与圆的交点B处小球具有最小动能EkB，设小球在复合场中所受的电场力为F，合力为F合，可知F合与竖直方向夹角为θ。
由A到B，根据动能定理，有：
解得小球受到重力和电场力的合力：
（2）在A点，有：
解得最大动能
则最小动能
（3）小球在B点时速度跟重力和电场力的合力垂直，撤去轨道后，小球做类平抛运动。
0．4s时间内，根据动能定理，有：
，又
可得小球沿BA方向的位移为
由
可得，小球质量
电场力
电场强度
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
