题目内容
 如图所示,边长为L的正方形线 圈abcd的匝数为n,线圈电阻为r,外电路的电阻为R,磁感应强度为B,电压表为理想交流电压表.现在线圈以角速度ω绕垂直于磁感线的对称轴OO′匀速转动,从线圈平面与磁感线平行开始计时.试求:
如图所示,边长为L的正方形线 圈abcd的匝数为n,线圈电阻为r,外电路的电阻为R,磁感应强度为B,电压表为理想交流电压表.现在线圈以角速度ω绕垂直于磁感线的对称轴OO′匀速转动,从线圈平面与磁感线平行开始计时.试求:(1)闭合电路中电流瞬时值的表达式;
(2)电压表的示数
(3)线圈从t=0开始,转过900的过程中,电阻R上通过的电荷量.
分析:(1)根据公式Em=nBSω求出感应电动势的最大值,由欧姆定律求出感应电流的最大值Im.从线圈平面与磁感线平行开始计时,电流瞬时值的表达式e=Imcosωt.
(2)电压表测量R两端电压的有效值.
(3)根据法拉第电磁感应定律、欧姆定律和电流公式求出电阻R上通过的电荷量.
(2)电压表测量R两端电压的有效值.
(3)根据法拉第电磁感应定律、欧姆定律和电流公式求出电阻R上通过的电荷量.
解答:解:(1)线圈转动时,电动势的最大值Em=nBωL2
由闭合电路的欧姆定律得:
电流最大值Im=
故闭合电路中电流瞬时值的表达式为:i=
cosωt
(2)电路中电流的有效值I=
?
则电压表的示数U=IR=
?
(3)因R与线圈串联,则电阻R上通过的电荷量与通过线圈的电量相等
因q=
?△t,
=
=
所以q=
=
答:
(1)闭合电路中电流瞬时值的表达式为i=
cosωt;
(2)电压表的示数为
?
(3)线圈从t=0开始,转过90°的过程中,电阻R上通过的电荷量
.
由闭合电路的欧姆定律得:
电流最大值Im=
| nBωL2 |
| R+r |
故闭合电路中电流瞬时值的表达式为:i=
| nBωL2 |
| R+r |
(2)电路中电流的有效值I=
| ||
| 2 |
| nBωL2 |
| R+r |
则电压表的示数U=IR=
| ||
| 2 |
| nBRωL2 |
| R+r |
(3)因R与线圈串联,则电阻R上通过的电荷量与通过线圈的电量相等
因q=
. |
| I |
. |
| I |
| ||
| R+r |
| n△φ |
| (r+R)△t |
所以q=
| n△φ |
| R+r |
| nBπL2 |
| R+r |
答:
(1)闭合电路中电流瞬时值的表达式为i=
| nBωL2 |
| R+r |
(2)电压表的示数为
| ||
| 2 |
| nBRωL2 |
| R+r |
(3)线圈从t=0开始,转过90°的过程中,电阻R上通过的电荷量
| nBπL2 |
| R+r |
点评:当从中性开始计时时,电流瞬时值的表达式为i=Imsinωt;从线圈平面与磁感线平行开始计时,电流瞬时值的表达式为i=Imcosωt.

练习册系列答案
相关题目
 如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计带电粒子的重力.
如图所示,边长为L的正方形区域abcd内存在着匀强电场.电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场,不计带电粒子的重力. 如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )
如图所示,边长为L的正方形线图abcd匝数为n、电阻为r,外电路的电阻为R,线圈位于磁感应强度为B的匀强磁场中,若线圈从图示位置开始,以角速度ω绕OO′轴匀速转动,则以下判断中正确的是( )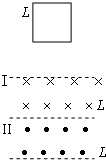 如图所示,边长为L的正方形导线框底边水平,且平行于正下方的磁场边界,正下方的匀强磁场宽度均为L,磁感强度等值反向,两磁场区域紧邻.当线框底边进入磁场I区域时,导线框恰好做匀速运动,这时导线框的电功率为P.则当导线框底边刚进入磁场II区域时,下列结论正确的是( )
如图所示,边长为L的正方形导线框底边水平,且平行于正下方的磁场边界,正下方的匀强磁场宽度均为L,磁感强度等值反向,两磁场区域紧邻.当线框底边进入磁场I区域时,导线框恰好做匀速运动,这时导线框的电功率为P.则当导线框底边刚进入磁场II区域时,下列结论正确的是( ) 如图所示,边长为L的正方形区域abcd内存在着匀强电场,一个质量为m、电量为q、初速度为v0的带电
如图所示,边长为L的正方形区域abcd内存在着匀强电场,一个质量为m、电量为q、初速度为v0的带电 如图所示,边长为L的正方形闭合线框,在磁感应强度为B的匀强磁场中,以一条边为轴,以角速度ω匀速转动,转轴与B垂直,线圈总电阻为R,导线电阻不计.下列说法中正确的是( )
如图所示,边长为L的正方形闭合线框,在磁感应强度为B的匀强磁场中,以一条边为轴,以角速度ω匀速转动,转轴与B垂直,线圈总电阻为R,导线电阻不计.下列说法中正确的是( )