题目内容
在光滑水平面上放置两长度相同、质量分别为m1和m2的木板P、Q,在木板的左端各有一大小、形状、质量完全相同的物块a和b,木板和物块均处于静止状态.现对物块a和b分别施加水平恒力F1和F2,使它们向右运动.当物块与木板分离时,P、Q的速度分别为v1、v2,物块a、b相对地面的位移分别为s1、s2.已知两物块与木板间的动摩擦因数相同,下列判断正确的是( )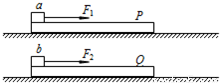
A.若F1=F2、m1>m2,则v1>v2、S1=S2
B.若F1=F2、m1<m2,则v1>v2、S1=S2
C.若F1>F2、m1=m2,则v1<v2、S1>S2
D.若F1<F2、m1=m2,则v1>v2、S1>S2
【答案】分析:本题中涉及到两个物体,所以就要考虑用整体法还是隔离法,但题中研究的是两物体的相对滑动,所以应该用隔离法.板和物体都做匀变速运动,牛顿定律加运动学公式和动能定理都能用,但题中“当物体与板分离时”隐含着在相等时间内物体的位移比板的位移多一个板长,也就是隐含着时间因素,所以不方便用动能定理解了,就要用牛顿定律加运动公式解.
解答:解:A、首先看F1=F2 时情况:
由题很容易得到a、b 所受的摩擦力大小是相等的,因此a、b 加速度相同,我们设a、b 加速度大小为a,
对于P、Q,滑动摩擦力即为它们的合力,设P(m1)的加速度大小为a1,Q(m2)的加速度大小为a2,
根据牛顿第二定律得:
因为a1=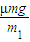 ,a2=
,a2=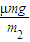 ,其中m为物块a和b的质量.
,其中m为物块a和b的质量.
设板的长度为L,它们向右都做匀加速直线运动,当物块与木板分离时:
a与P 的相对位移L= at12-
at12- a1t12
a1t12
b与Q 的相对位移L= at22-
at22- a2t22
a2t22
若m1>m2,a1<a2
所以得:t1<t2
P的速度为v1=a1t1,Q的速度为v2=a2t2
物块a相对地面的位移分别为s1= at12
at12
物块b相对地面的位移分别为s2= at22
at22
则v1<v2,s1<s2,故A、B错误.
C、若F1>F2、m1=m2,根据受力分析和牛顿第二定律的:
则a的加速度大于b的加速度,即aa>ab
由于m1=m2,所以P、Q加速度相同,设P、Q加速度为a.
它们向右都做匀加速直线运动,当物块与木板分离时:
a与P 的相对位移L= aat12-
aat12- at12
at12
b与Q 的相对位移L= abt22-
abt22- at22
at22
由于aa>ab
所以得:t1<t2
则v1<v2,s1<s2,故C错误.
D、根据C选项分析得:
若F1<F2、m1=m2,aa<ab
则v1>v2、S1>S2
故D正确.
故选D.
点评:要去比较一个物理量两种情况下的大小关系,我们应该通过物理规律先把这个物理量表示出来.
要把受力分析和牛顿第二定律结合应用.
解答:解:A、首先看F1=F2 时情况:
由题很容易得到a、b 所受的摩擦力大小是相等的,因此a、b 加速度相同,我们设a、b 加速度大小为a,
对于P、Q,滑动摩擦力即为它们的合力,设P(m1)的加速度大小为a1,Q(m2)的加速度大小为a2,
根据牛顿第二定律得:
因为a1=
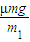 ,a2=
,a2=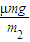 ,其中m为物块a和b的质量.
,其中m为物块a和b的质量.设板的长度为L,它们向右都做匀加速直线运动,当物块与木板分离时:
a与P 的相对位移L=
 at12-
at12- a1t12
a1t12b与Q 的相对位移L=
 at22-
at22- a2t22
a2t22若m1>m2,a1<a2
所以得:t1<t2
P的速度为v1=a1t1,Q的速度为v2=a2t2
物块a相对地面的位移分别为s1=
 at12
at12物块b相对地面的位移分别为s2=
 at22
at22则v1<v2,s1<s2,故A、B错误.
C、若F1>F2、m1=m2,根据受力分析和牛顿第二定律的:
则a的加速度大于b的加速度,即aa>ab
由于m1=m2,所以P、Q加速度相同,设P、Q加速度为a.
它们向右都做匀加速直线运动,当物块与木板分离时:
a与P 的相对位移L=
 aat12-
aat12- at12
at12b与Q 的相对位移L=
 abt22-
abt22- at22
at22由于aa>ab
所以得:t1<t2
则v1<v2,s1<s2,故C错误.
D、根据C选项分析得:
若F1<F2、m1=m2,aa<ab
则v1>v2、S1>S2
故D正确.
故选D.
点评:要去比较一个物理量两种情况下的大小关系,我们应该通过物理规律先把这个物理量表示出来.
要把受力分析和牛顿第二定律结合应用.

练习册系列答案
相关题目
在光滑水平面上放置两长度相同、质量分别为m1和m2的木板P、Q,在木板的左端各有一大小、形状、质量完全相同的物块a和b,木板和物块均处于静止状态。现对物块a和b分别施加水平恒力F1和F2,使它们向右运动。当物块与木板分离时,P、Q的速度分别为v1、v2,物块P、Q相对地面的位移分别为s1、s2。已知两物块与木板间的动摩擦因数相同,下列判断正确的是 ( )
A.若F1=F2、m1>m2,则 、 、 |
B.若F1=F2、m1<m2,则 、 、 |
C.若F1 > F2、m1=m2,则 、 、 |
D.若F1 < F2、m1=m2,则 、 、 |
 在光滑水平面上放置两长度相同、质量分别为m1和m2的木板P、Q,在木板的左端各有一大小、形状、质量完全相同的物块a和b,木板和物块均处于静止状态.现对物块a和b分别施加水平恒力F1和F2,使它们向右运动.当物块与木板分离时,P、Q的速度分别为v1、v2,物块a、b相对地面的位移分别为s1、s2.已知两物块与木板间的动摩擦因数相同,下列判断正确的是( )
在光滑水平面上放置两长度相同、质量分别为m1和m2的木板P、Q,在木板的左端各有一大小、形状、质量完全相同的物块a和b,木板和物块均处于静止状态.现对物块a和b分别施加水平恒力F1和F2,使它们向右运动.当物块与木板分离时,P、Q的速度分别为v1、v2,物块a、b相对地面的位移分别为s1、s2.已知两物块与木板间的动摩擦因数相同,下列判断正确的是( )
 、
、
 、
、
 、
、
