题目内容
完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)(1)铅块在第几块木块上运动时,能带动它右面的木块一起运动?
(2)小铅块最终是滑出所有木块,还是停在那块木块上?若停在木块上,求出铅块停在木块上的位置.

【答案】分析:(1)铅块在木块上滑行时,当铅块对木块的滑动摩擦力等于木块所受的最大静摩擦力时,恰好能带动它右面的木块一起运动.
(2)根据上题的结果,运用动能定理列式求出铅块滑上该木块左端时的速度,由牛顿第二定律求出铅块和已滑动的木块整体的加速度.由运动学公式求出铅块相对木块静止时滑行的距离,即可进行判断.
解答:解:(1)木块受到铅块提供的滑动摩擦力f=μ2Mg=2.0N
有铅块的那个木块与地面间的最大静摩擦力为f1=μ1(M+m)g=1.4N
其余每个木块与地面间的最大静摩擦力为f2=μ1mg=0.4N
设铅块到第n个木块时,第n个木块及后面的木块开始在地面上滑动,则
f>(13-n)f2+f1,
得 n>11.5
即当铅块滑到第12个木块左端时,12、13两木块开始在地面上滑动.
(2)铅块刚滑上第12个木块左端时的速度v1,由动能定理得
-μ2Mg?11L=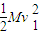 -
-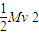
解得v1=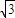 m/s
m/s
铅块滑动的加速度a=- =-μ2g=-2m/s2
=-μ2g=-2m/s2
此时第12、13的加速度a1= =0.25m/s2
=0.25m/s2
以第12、13两木块为参考系,铅块滑到第12个木块右端时相对木块的速度v2满足
 =2(a-a1)L
=2(a-a1)L
解得,v2=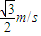 >0
>0
故铅块可以滑上第13个木块,在第13个木块上滑动时,木块的加速度为
a2= =1.5m/s2
=1.5m/s2
以第13个木块为参照,铅块相对木块13静止时滑行的距离为s=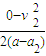 =0.107m<L
=0.107m<L
所以,铅块最终停在第13块木块上,距离其左端0.107m.
答:
(1)铅块在第12块木块上运动时,能带动它右面的木块一起运动.
(2)铅块最终停在第13块木块上,距离其左端0.107m.
点评:本题是牛顿第二定律、运动学和动能定理、摩擦力公式等等知识的综合应用,关键通过分析受力,判断木块的状态.
(2)根据上题的结果,运用动能定理列式求出铅块滑上该木块左端时的速度,由牛顿第二定律求出铅块和已滑动的木块整体的加速度.由运动学公式求出铅块相对木块静止时滑行的距离,即可进行判断.
解答:解:(1)木块受到铅块提供的滑动摩擦力f=μ2Mg=2.0N
有铅块的那个木块与地面间的最大静摩擦力为f1=μ1(M+m)g=1.4N
其余每个木块与地面间的最大静摩擦力为f2=μ1mg=0.4N
设铅块到第n个木块时,第n个木块及后面的木块开始在地面上滑动,则
f>(13-n)f2+f1,
得 n>11.5
即当铅块滑到第12个木块左端时,12、13两木块开始在地面上滑动.
(2)铅块刚滑上第12个木块左端时的速度v1,由动能定理得
-μ2Mg?11L=
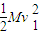 -
-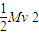
解得v1=
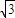 m/s
m/s铅块滑动的加速度a=-
 =-μ2g=-2m/s2
=-μ2g=-2m/s2此时第12、13的加速度a1=
 =0.25m/s2
=0.25m/s2以第12、13两木块为参考系,铅块滑到第12个木块右端时相对木块的速度v2满足
 =2(a-a1)L
=2(a-a1)L解得,v2=
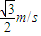 >0
>0故铅块可以滑上第13个木块,在第13个木块上滑动时,木块的加速度为
a2=
 =1.5m/s2
=1.5m/s2以第13个木块为参照,铅块相对木块13静止时滑行的距离为s=
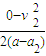 =0.107m<L
=0.107m<L所以,铅块最终停在第13块木块上,距离其左端0.107m.
答:
(1)铅块在第12块木块上运动时,能带动它右面的木块一起运动.
(2)铅块最终停在第13块木块上,距离其左端0.107m.
点评:本题是牛顿第二定律、运动学和动能定理、摩擦力公式等等知识的综合应用,关键通过分析受力,判断木块的状态.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)
完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.) 完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)
完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)