题目内容
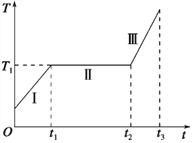
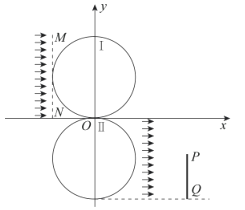
【题目】如图所示的两个圆形磁场可实现带电粒子的汇聚与侧移。在x-y轴直角坐标平面内,两个圆形磁场Ⅰ、Ⅱ相切于坐标原点O,圆心均在y轴上,半径均为R,磁感应强度大小相等,垂直于x-y轴直角坐标平面且方向相反。大量带正电的粒子质量为m,带电量为q,以平行于x轴的速度v沿x轴正方向进入磁场Ⅰ,经磁场偏转后汇聚于坐标原点O并进入磁场Ⅱ,经磁场Ⅱ再次偏转后以平行于x轴的方向离开磁场Ⅱ实现侧移。在x轴下方有一平行于y轴的长度为R的粒子收集板PQ,Q点的坐标为(2R,-2R)。粒子打在收集板上被吸收不影响其他粒子的运动。不计粒子重力及粒子间的相互作用。
(1)求磁场Ⅰ的磁感应强度B的大小和方向;
(2)虚线MN平行于y轴且与磁场Ⅰ相切,经过MN上纵坐标为1.5R的点的粒子能否打在收集板上?若不能,请说明理由。若能,求其从MN到PQ的时间;
(3)假设收集板上端P点与x轴之间的距离d可在0与R之间变化,写出从MN到PQ的粒子打在Q点的运动时间T1和打在P点时间T2关于d的关系式。(解题中涉及的角度可用余弦的反三角函数表示,如![]() )
)
【答案】(1)![]() ,方向垂直x-y轴直角坐标平面向外;(2)能,
,方向垂直x-y轴直角坐标平面向外;(2)能,![]() ;(3)
;(3)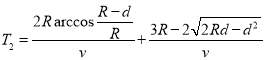
【解析】
(1)欲使带电粒子汇聚于O点并实现侧移,由几何关系可知,粒子在磁场中做匀速圆周运动的半径为R,根据
![]()
可得
![]()
方向垂直x-y轴直角坐标平面向外。
(2)粒子的运动轨迹如图1所示,
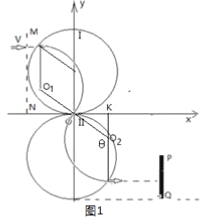
由几何关系可知,粒子在每个磁场中的运动圆心角θ均为![]() ,故粒子在磁场中的运动时间为
,故粒子在磁场中的运动时间为
![]()
粒子在磁场外的运动时间为
![]()
所以粒子从MN到PQ的时间为
![]()
(3)当PQ上端P点与x轴的距离为d时,从MN到PQ的粒子打在Q点的粒子运动时间最长。打在Q点的粒子运动轨迹如图2所示
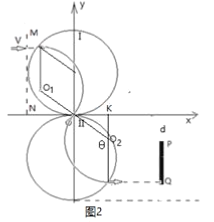
O1和O2分别为其在磁场ⅠⅡ中做圆周运动的圆心,其在磁场中的轨迹关于O点对称。过O2作O2K垂直X轴,在三角形O2KO中
![]()
则粒子在一个磁场中运动的圆心角
![]()
所以
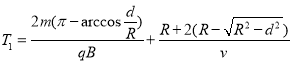
![]()
从MN到PQ的粒子打在P点的粒子运动时间最短。打在P点的粒子运动轨迹如图3所示,
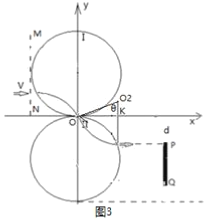
O2为其在磁场Ⅱ中做圆周运动的圆心,在三角形O2KO中,粒了在一个磁场中运动的圆心角
![]()
则
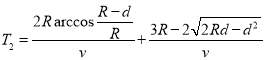

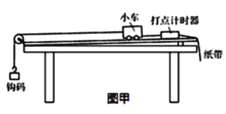
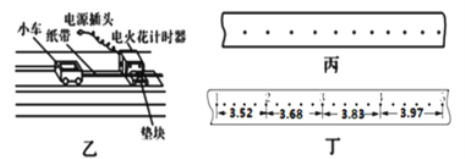
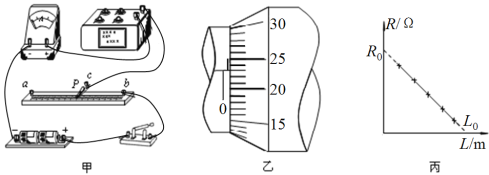
【题目】为测量木块与木板间的动摩擦因数,将木反倾斜,木块以不同的初速度沿木板向上滑到最高点后再返回,用光电门测量木块来回的速度,用刻度尺测量向上运动的最大距离,为确定木块向上运动的最大高度,让木块推动轻质卡到最高点,记录这个位置,实验装置如图甲所示.
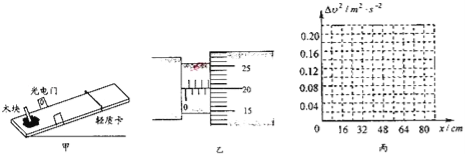
(1)本实验中,下列操作合理的是
A.遮光条的宽度应尽量小些 |
B.实验前将轻质卡置于光电门附近 |
C.为了实验成功,木块的倾角必须大于某一值 |
D.光电门与轻质卡最终位置间的距离即为木块向上运动的最大距离 |
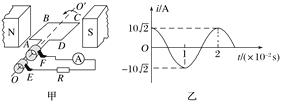
(2)用螺旋测微器测量遮光条的宽度,如图乙所示读数为 mm.
(3)改变木块的初速度,测量出它向上运动的最大距离与木块来回经过光电门时速度的平方差,结果如下表所示,试在丙图坐标纸上作出△v2﹣x的图象,经测量木板倾角的余弦值为0.6,重力加速度取g=9.80m/s2,则木块与木板间的动摩擦因数为 (结果保留两位有效数字).
序号 | 1 | 2 | 3 | 4 | 5 |
X/cm | 16.0 | 36.0 | 60.0 | 70.0 | 88.0 |
△v2/m2s﹣2 | 0.04 | 0.09 | 0.15 | 0.19 | 0.22 |
(4)由于轻质卡的影响,使得测量的结果 (选填“偏大”或“偏小”).