题目内容
1.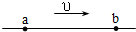 如图所示,一根张紧的水平弹性绳上的a、b两点,相距14.0m,a、b两点的距离小于一个波长,b点在a点右方,当一列简谐波沿此长绳向右传播时,若a点的位移达到正向最大时,b点的位移为零且向下运动,经过1s后a点的位移为零,且向下运动,而b点的位移恰达到负最大.则这简谐波的波速可能等于( )
如图所示,一根张紧的水平弹性绳上的a、b两点,相距14.0m,a、b两点的距离小于一个波长,b点在a点右方,当一列简谐波沿此长绳向右传播时,若a点的位移达到正向最大时,b点的位移为零且向下运动,经过1s后a点的位移为零,且向下运动,而b点的位移恰达到负最大.则这简谐波的波速可能等于( )| A. | 12米/秒 | B. | 22米/秒 | C. | 32米/秒 | D. | 42米/秒 |
分析 根据a、b两点的状态:a点的位移达到正向最大时,b点的位移恰好为零,且向下运动,确定出波长与ab距离的关系,得到波长的通项.根据时间与周期的关系,得到周期的通项,求出波速的通项,再求解特殊值.
解答 解:由题,简谐波沿绳向右传播时,若a点的位移达到正向最大时,b点的位移恰好为零,且向下运动,结合波形得到:
△x=(n+$\frac{3}{4}$)λ,n=0,1,2,…
得到波长通项为:λ=$\frac{4△x}{4n+3}$=$\frac{56}{4n+3}$m/s.
又由题,经过1.00s后,a点的位移为零,且向下运动,则有:
△t=(k+$\frac{1}{4}$)T,k=0,1,2,…
得到周期的通项为:T=4$\frac{△t}{4k+1}$=$\frac{4}{4k+1}$s
则波速为v=$\frac{λ}{T}$=$\frac{14(4k+1)}{4n+3}$m/s
当n=0,k=0时,v=4.67m/s;
当n=0,k=1时,v=23.3m/s.
当n=0,k=2时,v=42m/s.
当n=1,k=1时,v=10m/s.
当n=1,k=2时,v=18m/s.故ABC错误,D正确;
故选:D.
点评 本题考查运用数学知识列出波长、周期和波速通项的能力,要结合波形分析距离与波长的关系.

练习册系列答案
相关题目
16.用手握紧竖直的瓶子,使瓶子不掉下来,下列说法正确的是( )
| A. | 手对瓶子的摩擦力大于瓶子的重力 | |
| B. | 增大手对瓶子的压力,手对瓶子的摩擦力不变 | |
| C. | 瓶子受到的合力可以不为零 | |
| D. | 瓶子受到手的压力的合力为零 |
6.关于第一宇宙速度,下列说法哪些是正确的?( )
| A. | 它是人造卫星绕地球做匀速圆周运动的最小运行速度 | |
| B. | 这是人造卫星绕地球做匀速圆周运动的最大运行速度 | |
| C. | 它是人造卫星绕地球飞行所需的最小水平发射速度 | |
| D. | 它是人造卫星绕地球飞行所需的最大水平发射速度 |
13. 如图所示,轻弹簧的两端各受10N拉力F作用,弹簧平衡时伸长了5cm(在弹性限度内);那么下列说法中正确的是( )
如图所示,轻弹簧的两端各受10N拉力F作用,弹簧平衡时伸长了5cm(在弹性限度内);那么下列说法中正确的是( )
 如图所示,轻弹簧的两端各受10N拉力F作用,弹簧平衡时伸长了5cm(在弹性限度内);那么下列说法中正确的是( )
如图所示,轻弹簧的两端各受10N拉力F作用,弹簧平衡时伸长了5cm(在弹性限度内);那么下列说法中正确的是( )| A. | 该弹簧的劲度系数k=200N/m | |
| B. | 该弹簧的劲度系数k=400N/m | |
| C. | 弹簧所受的合力为0 | |
| D. | 根据公式k=$\frac{F}{x}$,弹簧的劲度系数k会随弹簧弹力F的增大而增大 |
10.关于速度和加速度的关系,下列说法中不正确的是( )
| A. | 速度很大,加速度可能是零 | B. | 速度为零,加速度不一定为零 | ||
| C. | 速度很小,加速度可能很大 | D. | 速度变化越大,加速度就一定越大 |
11.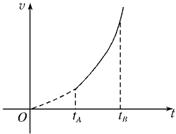 一正电荷在电场中仅在电场力作用下,从A点运动到B点,速度大小随时间变化的图象如图所示,tA、tB分别是电荷在A、B两点对应的时刻,则下列说法中正确的有( )
一正电荷在电场中仅在电场力作用下,从A点运动到B点,速度大小随时间变化的图象如图所示,tA、tB分别是电荷在A、B两点对应的时刻,则下列说法中正确的有( )
 一正电荷在电场中仅在电场力作用下,从A点运动到B点,速度大小随时间变化的图象如图所示,tA、tB分别是电荷在A、B两点对应的时刻,则下列说法中正确的有( )
一正电荷在电场中仅在电场力作用下,从A点运动到B点,速度大小随时间变化的图象如图所示,tA、tB分别是电荷在A、B两点对应的时刻,则下列说法中正确的有( )| A. | A处的场强一定小于B处的场强 | |
| B. | A处的电势一定高于B处的电势 | |
| C. | 电荷在A处的电势能一定小于B处的电势能 | |
| D. | A至B过程中,电荷的机械能一定守恒 |
 如图,质量为m的小球从高为R的斜面的顶端无初速下滑,斜面与水平面的夹角为45°,小球经过水平地面后滑上光滑的半圆弧,半圆弧与水平面相切,圆弧的半径为R,不计小球从斜面滑上水平面损失的机械能,整个轨道绝缘.整个装置处于电场强度为E的水平匀强电场中,轨道平面与电场平行.小球与斜面和水平面的动摩擦因素为0.5,小球在斜面上没受摩擦力,小球到圆弧顶端时撤去电场,此时小球恰不受压力.求:
如图,质量为m的小球从高为R的斜面的顶端无初速下滑,斜面与水平面的夹角为45°,小球经过水平地面后滑上光滑的半圆弧,半圆弧与水平面相切,圆弧的半径为R,不计小球从斜面滑上水平面损失的机械能,整个轨道绝缘.整个装置处于电场强度为E的水平匀强电场中,轨道平面与电场平行.小球与斜面和水平面的动摩擦因素为0.5,小球在斜面上没受摩擦力,小球到圆弧顶端时撤去电场,此时小球恰不受压力.求: 如图所示,水平地面的上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.
如图所示,水平地面的上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.