Question

如图7-6-3所示，半径为R、内表面光滑的细圆管固定在竖直面上，管内最低点有一质量为m的小球以速度v₀沿管做圆周运动.求：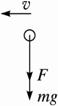

图7-6-3

（1）小球通过圆管最高点时的速度大小；

（2）小球通过圆管最高点时对管壁的压力.

Answer 1

解析：（1）由于球在光滑细管中运动时，管对球的弹力总是和运动方向垂直，弹力对球不做功，球在管内运动时机械能守恒.以球在最低点为零势能点，则

m=mg·2R+mv²

    球通过圆管的最高点时的速度为：v=.

（2）设球在最高点时对管外壁向上的压力为F′，则管对球的作用力大小为F，方向竖直向下（如图），由牛顿第二定律得F+mg=m,F=m-5mg

    讨论：①当m＞5mg,

    即v₀＞时，球在最高点对管的压力向上.

②当m=5mg,

    即v₀=时，球在最高点对管的压力为零.

③m＜5mg，

    即v₀＜时，球在最高点对管的压力向下.