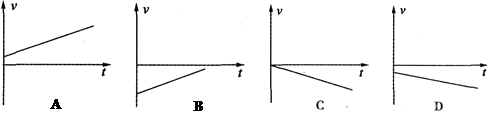
题目内容
如图所示,某生产线上相互垂直的甲、乙传送带等高,宽度均为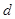 ,而且均以大小为
,而且均以大小为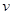 的速度运行,图中虚线为传送带中线。一工件(视为质点)从甲左端释放,经长时间由甲右端滑上乙,滑至乙中线处时恰好相对乙静止。下列说法中正确的是 ( )
的速度运行,图中虚线为传送带中线。一工件(视为质点)从甲左端释放,经长时间由甲右端滑上乙,滑至乙中线处时恰好相对乙静止。下列说法中正确的是 ( )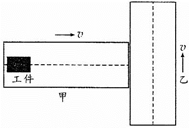
A.工件在乙传送带上的痕迹为直线,痕迹长为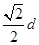 |
B.工件从滑上乙到恰好与乙相对静止所用的时间为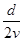 |
C.工件与乙传送带间的动摩擦因数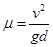 |
| D.乙传送带对工件的摩擦力做功为零 |
AD
解析试题分析:物体滑上乙时,相对于乙上的那一点的速度分为水平向右的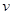 和向后的
和向后的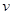 ,合速度为
,合速度为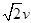 ,就是沿着与乙成45°的方向,那么相对于乙的运动轨迹肯定是直线,故A正确。假设它受滑动摩擦力
,就是沿着与乙成45°的方向,那么相对于乙的运动轨迹肯定是直线,故A正确。假设它受滑动摩擦力 ,方向与合相对速度在同一直线,所以角
,方向与合相对速度在同一直线,所以角 ,则相对于乙的加速度也沿这个方向,经过t后,它滑到乙中线并相对于乙静止,根据牛顿第二定律,有:
,则相对于乙的加速度也沿这个方向,经过t后,它滑到乙中线并相对于乙静止,根据牛顿第二定律,有: ,解得
,解得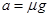 ;运动距离
;运动距离 又
又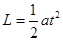 ,L和a代入所以
,L和a代入所以 ,
, ,故B错误、C错误。滑上乙之前,工件绝对速度为
,故B错误、C错误。滑上乙之前,工件绝对速度为 ,动能为
,动能为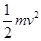 ,滑上乙并相对停止后,绝对速度也是
,滑上乙并相对停止后,绝对速度也是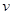 ,动能也是
,动能也是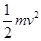 ,而在乙上面的滑动过程只有摩擦力做了功,动能又没变化,所以乙对工件的摩擦力做功为0,故D正确。
,而在乙上面的滑动过程只有摩擦力做了功,动能又没变化,所以乙对工件的摩擦力做功为0,故D正确。
考点:本题考查了牛顿第二定律、匀变速直线运动的规律、动能定理.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案一个质点正在作匀加速直线运动,用固定在地面上的照相机对该质点进行闪光照相,闪光时间间隔为1s,分析照片得到的数据,发现质点在第1次、第2次闪光的时间间隔内移动了2m;第3次、第4次时间间隔内移动了8m;由此可以求出
| A.质点运动的初速度 |
| B.质点运动加速度 |
| C.第1次闪光时质点的速度 |
| D.从第2次闪光到第3次闪光这段时间内质点的位移 |
如图所示,甲、乙两小球沿光滑轨道ABCD运动。在轨道水平段AB上运动时,两小球的速度均为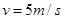 ,相距
,相距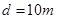 ;轨道水平段AB和水平段CD的高度差为
;轨道水平段AB和水平段CD的高度差为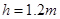 ;水平段与斜坡段间均有光滑小圆弧连接,且两小球在运动中始终未脱离轨道。关于两小球在轨道水平段CD上的运动情况,下列描述中正确的是( )
;水平段与斜坡段间均有光滑小圆弧连接,且两小球在运动中始终未脱离轨道。关于两小球在轨道水平段CD上的运动情况,下列描述中正确的是( )
A.两小球在CD段运动时仍相距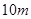 |
B.两小球在CD段运动时距离小于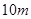 |
C.两小球到达图示位置P点的时间差为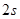 |
D.两小球到达图示位置P点的时间差小于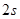 |
如图所示,t=0时,质量为0.5 kg物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设物体经过B点前后速度大小不变),最后停在C点.测得每隔2 s的三个时刻物体的瞬时速度记录在表格中,由此可知(重力加速度g=10 m/s2) ( ) 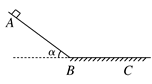
| t/s | 0 | 2 | 4 | 6 |
| v/m·s 1 | 0 | 8 | 12 | 8 |
B.t=3 s的时刻物体恰好经过B点
C.t=10 s的时刻物体恰好停在C点
D.A、B间的距离大于B、C间的距离
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d四点,总时间是t,下列说法不正确的是( )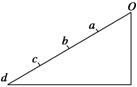
A.质点由O到达各点的时间之比ta∶tb∶tc∶td=1∶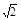 ∶ ∶ ∶2 ∶2 |
B.质点通过各点的速率之比va∶vb∶vc∶vd=1∶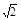 ∶ ∶ ∶2 ∶2 |
C.在斜面上运动的平均速度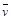 =vb =vb |
D.在斜面上运动的平均速度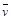 =vd/2 =vd/2 |
如图,光滑斜面AE被分成四个相等的部分,一个物体由A点静止释放,下面结论中正确的是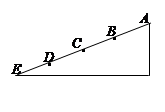
| A.物体到达各点的速度vB: vC:vD::vE=1:21/2:31/2:2 |
| B.物体到达各点所经历的时间tB: tC:tD::tE=1:21/2:31/2:2 |
| C.物体从A到E的平均速度v=vB |
| D.经过每一部分时,其速度增量均相同 |