题目内容
11.两列火车相向而行.甲车速率为60km/h,乙车速率为40km/h,当两车相距为50km时.甲车上有一只鸟以80km/h的速率飞向乙车,设它遇到乙车后立即以同样的大小的速率返回甲车,然后以同样的速率再返问乙车,如此往复运动,直到甲、乙两车相遇,求在此过程中鸟共飞了多长的路程?分析 甲乙两列火车相向运动,相遇的时间即为鸟飞行的时间,根据位移关系求出相遇的时间,根据鸟的速度求出鸟飞行的路程.
解答 解:两车相遇的时间t=$\frac{x}{{v}_{1}+{v}_{2}}=\frac{50}{60+40}h=0.5h$,
则鸟飞行的路程s=v3t=80×0.5km=40km.
答:在此过程中鸟共飞了40km.
点评 解决本题的关键知道鸟飞行的时间与两车相遇的时间相等,根据位移求出相遇时间是关键.

练习册系列答案
相关题目
2.手拖动纸带经过打点计时器后,在纸带上留下的点中有6个连续清晰的点A,B,C,D,E,F,测得AB=2cm,BC=4cm,CD=3cm,DE=2.8cm,EF=6cm,则BF段测得平均速度为( )
| A. | 平均速度为0.198m/s | B. | 平均速度为1.98m/s | ||
| C. | 平均速度为1.98cm/s | D. | 平均速度为198m/s |
16. 如图所示,长为l的光滑直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一挡板,杆与板面垂直,滑块与挡板碰撞后以碰撞前速率的一半返回,现将滑块拉到A点由静止释放,设重力加速度为g,则( )
如图所示,长为l的光滑直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一挡板,杆与板面垂直,滑块与挡板碰撞后以碰撞前速率的一半返回,现将滑块拉到A点由静止释放,设重力加速度为g,则( )
 如图所示,长为l的光滑直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一挡板,杆与板面垂直,滑块与挡板碰撞后以碰撞前速率的一半返回,现将滑块拉到A点由静止释放,设重力加速度为g,则( )
如图所示,长为l的光滑直杆AB与水平面成α角固定,在杆上套一质量为m的小滑块,杆底端B点处有一挡板,杆与板面垂直,滑块与挡板碰撞后以碰撞前速率的一半返回,现将滑块拉到A点由静止释放,设重力加速度为g,则( )| A. | 可以确定滑块最终所处的位置 | |
| B. | 可以确定滑块从释放到停止运动的总路程 | |
| C. | 可以确定滑块从第k次碰撞后到第(k+1)次与挡板碰撞所需的时间 | |
| D. | 可以判断滑块每次与挡板碰撞损失的机械能相同 |

 如图所示一质点做匀变速直线运动,在通过a点时,速度大小为Va=4m/s,方向向右(规定为正方向),经过t=1s后,该质点在b,速度Vb的大小为4m/s.
如图所示一质点做匀变速直线运动,在通过a点时,速度大小为Va=4m/s,方向向右(规定为正方向),经过t=1s后,该质点在b,速度Vb的大小为4m/s.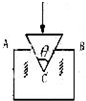 如图所示,一表面光滑质量很小的截面是等腰三角形的尖劈,其顶角C为θ,把它插在缝A、B之间,如图所示,在尖劈上加一压力F,则尖劈对缝的左或右侧的压力大小为$\frac{F}{{2sin\frac{θ}{2}}}$.
如图所示,一表面光滑质量很小的截面是等腰三角形的尖劈,其顶角C为θ,把它插在缝A、B之间,如图所示,在尖劈上加一压力F,则尖劈对缝的左或右侧的压力大小为$\frac{F}{{2sin\frac{θ}{2}}}$.