题目内容
19.某人造卫星运动的轨道可近似看作是以地心为中心的圆.由于阻力作用,人造卫星到地心的距离从r1慢慢变到r2,用Ek1、Ek2分别表示卫星在这两个轨道上的动能,E1、E2表示卫星在这两个轨道上的机械能,则( )| A. | r1<r2,Ek1<Ek2,E1<E2 | B. | r1>r2,Ek1<Ek2,E1>E2 | ||
| C. | r1>r2,Ek1>Ek2,E1<E2 | D. | r1<r2,Ek1>Ek2,E1>E2 |
分析 卫星要克服阻力做功,机械能减小,故卫星轨道半径变小,卫星绕地球做圆周运动,根据万有引力提供圆周运动向心力得出线速度的变化,从而得出动能的变化.
解答 解:卫星在圆轨道上做圆周运动,克服阻力做功,轨道半径减小,可知r1>r2,根据功能关系知,机械能减小,即E1>E2,
根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$知,v=$\sqrt{\frac{GM}{r}}$,轨道半径减小,则速度增大,所以Ek1<Ek2.
故选:B.
点评 卫星克服阻力做功使卫星做近心运动轨道半径减小,卫星在自自圆轨道上圆周运动万有引力提供圆周运动向心力,熟悉掌握向心力的不同表达式是正确解决问题的关键.

练习册系列答案
相关题目
5. 2016年9月19号,我国利用长征六号火箭成功发射了20颗小卫星,这种一箭多星技术是我国航天人长期坚持自主创新.刻苦攻关的结果,体现了我国航天人勇于探索太空的信心与决心,假设此次发射中有A、B两颗均绕地球作匀速圆周运动的卫星,如图所示,其中A星离地高度HA=100km,B星离地高度HB=200km,已知地球半径为6400km,有关A,B两颗卫星的说法正确的是( )
2016年9月19号,我国利用长征六号火箭成功发射了20颗小卫星,这种一箭多星技术是我国航天人长期坚持自主创新.刻苦攻关的结果,体现了我国航天人勇于探索太空的信心与决心,假设此次发射中有A、B两颗均绕地球作匀速圆周运动的卫星,如图所示,其中A星离地高度HA=100km,B星离地高度HB=200km,已知地球半径为6400km,有关A,B两颗卫星的说法正确的是( )
 2016年9月19号,我国利用长征六号火箭成功发射了20颗小卫星,这种一箭多星技术是我国航天人长期坚持自主创新.刻苦攻关的结果,体现了我国航天人勇于探索太空的信心与决心,假设此次发射中有A、B两颗均绕地球作匀速圆周运动的卫星,如图所示,其中A星离地高度HA=100km,B星离地高度HB=200km,已知地球半径为6400km,有关A,B两颗卫星的说法正确的是( )
2016年9月19号,我国利用长征六号火箭成功发射了20颗小卫星,这种一箭多星技术是我国航天人长期坚持自主创新.刻苦攻关的结果,体现了我国航天人勇于探索太空的信心与决心,假设此次发射中有A、B两颗均绕地球作匀速圆周运动的卫星,如图所示,其中A星离地高度HA=100km,B星离地高度HB=200km,已知地球半径为6400km,有关A,B两颗卫星的说法正确的是( )| A. | A、B两星的线速度之比$\sqrt{2}$:1 | |
| B. | A、B两星周期之比1:2$\sqrt{2}$ | |
| C. | A、B两星加速度之比662:652 | |
| D. | 由于阻力的作用,在A星逐渐进入大气层过程中,速度越来越大. |
6.如图甲所示,在x轴上有一个点电荷Q(图中未画出),O、A、B为轴上三点.放在A、B两点的检验电荷受到电场力与其所带电荷量的关系如图乙所示.以x轴的正方向为电场力的正方向,则( )
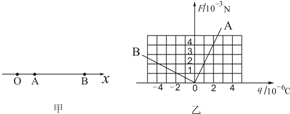

| A. | 点电荷Q一定为正电荷 | |
| B. | 点电荷Q在AB之间 | |
| C. | A点的电场强度大小为5×103N/C | |
| D. | 移走检验电荷后电场A、B两点的场强变为零 |
14.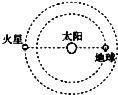 2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
 2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )
2013年4月出现“火星合日”的天象,“火星合日”是指火星、太阳、地球三者之间形成一条直线时,从地球的方位观察,火星位于太阳的正后方,火星被太阳完全遮蔽的现象,如图所示;已知地球、火星绕太阳运行的方向相同,若把火星和地球绕太阳运行的轨道视为圆,火星绕太阳公转周期约等于地球公转周期的2倍,由此可知( )| A. | “火星合日”约每1年出现一次 | |
| B. | “火星合日”约每4年出现一次 | |
| C. | 火星的公转半径约为地球公转半径的$\root{3}{4}$倍 | |
| D. | 火星的公转半径约为地球公转半径的8倍 |
4.在“探究加速度与力、质量的关系”实验中为了研究加速度跟力和质量的关系,应该采用的研究实验方法是( )
| A. | 控制变量法 | B. | 假设法 | C. | 理想实验法 | D. | 图象法 |
11. 阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
 阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )
阴极射线示波管的聚焦电场是由电极A1、A2形成的,其中虚线为等势线,相邻等势线间电势差相等,z轴为该电场的中心轴线(管轴).电子束从左侧进入聚焦电场后,在电场力的作用下会聚到z轴上,沿管轴从右侧射出,图中PQR是一个从左侧进入聚焦电场的电子运动轨迹上的三点,则可以确定( )| A. | 电极A1的电势高于电极A2的电势 | |
| B. | 电场中Q点的电场强度小于R点的电场强度 | |
| C. | 电子在R点处的动能小于在P点处的动能 | |
| D. | 若将一束带正电的粒子从左侧射入聚焦电场也一定被会聚 |
8.关于分子力和分子势能,下列说法正确的是( )
| A. | 分子间同时存在着引力和斥力 | |
| B. | 分子间的引力和斥力都是随着分子间距离的增大而减小 | |
| C. | 分子间的引力和斥力都是随着分子间距离的增大而增大 | |
| D. | 当分子力表现为引力时,分子势能总是随分子间距离的增大而减小 | |
| E. | 当分子力表现为引力时,分子势能总是随分子间距离的增大而增大 |
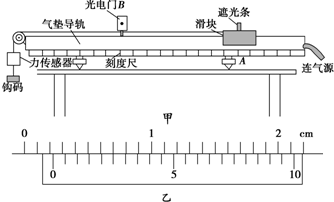 如图甲所示是某同学探究加速度与力的关系的实验装置.他在气垫导轨上安装了一个光电门B,在滑块上固定一遮光条,滑块用细线绕过气垫导轨左端的定滑轮与力传感器相连(力传感器可测得细线上的拉力大小),力传感器下方悬挂钩码,每次滑块都从A处由静止释放.
如图甲所示是某同学探究加速度与力的关系的实验装置.他在气垫导轨上安装了一个光电门B,在滑块上固定一遮光条,滑块用细线绕过气垫导轨左端的定滑轮与力传感器相连(力传感器可测得细线上的拉力大小),力传感器下方悬挂钩码,每次滑块都从A处由静止释放.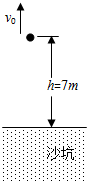 距沙坑高h=7m处,以v0=10m/s的初速度竖直向上抛出一个质量为0.5kg的物体,物体落到沙坑并陷入沙坑d=0.4m深处停下.不计空气阻力,重力加速度g=10m/s2.求:
距沙坑高h=7m处,以v0=10m/s的初速度竖直向上抛出一个质量为0.5kg的物体,物体落到沙坑并陷入沙坑d=0.4m深处停下.不计空气阻力,重力加速度g=10m/s2.求: