Question

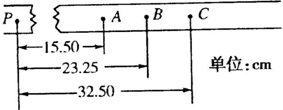在“用打点计时器验证机械能守恒定律”的实验中，质量m=1.00kg的重物拖着纸带竖直下落，打点计时器在纸带上打下一系列的点，如图所示．相邻计数点时间间隔为0.04s，P为纸带运动的起点，从P点到打下B点过程中物体重力势能的减少△Ep=

2.28

J，在此过程中物体动能的增加量△E_K=

2.26

J．（已知当地的重力加速度g=9.80m/s²，答案保留三位有效数字）用V表示各计数点的速度，h表示各计数点到P点的距离，以

V2

2

为纵轴，以h为横轴，根据实验数据绘出

V2

2

-h的图线，若图线的斜率等于某个物理量的数值时，说明重物下落过程中机械能守恒，该物理量是

当地重力加速度g

．

Answer 1

分析：利用匀变速直线运动的推论，可计算出打出某点时纸带运动的瞬时速度，从而求出动能．根据功能关系得重力势能减小量等于重力做功的数值．
要能够找出斜率和截距的物理意义，我们必须要从物理角度找出两个物理变量的关系表达式．

解答：解：根据重力势能的定义式得出：
从点p到打下计数点D的过程中，重锤重力势能减小量△E_P=mgh=1.0×9.8×0.2325 J=2.28 J
利用匀变速直线运动的推论
v_B=

xAC

tAC

=

(0.3250-0.1550)m

2×0.04s

=2.13m/s
E_kB=

1

2

mv_B²=0.2.26 J
此过程中物体动能的增加量△E_K=E_kB-0=0.2.26 J．
利用

1

2

v²-h图线处理数据，物体自由下落过程中机械能守恒，mgh=

1

2

mv²，即

1

2

v²=gh
所以以

1

2

v²为纵轴，以h为横轴画出的图线应是过原点的倾斜直线．
那么

1

2

v²-h图线的斜率就等于当地重力加速度g．
故答案为：2.28，2.26，当地重力加速度g．

点评：对于物理量线性关系图象的应用我们要从两方面：1、从物理角度找出两变量之间的关系式2、从数学角度找出图象的截距和斜率，两方面结合解决问题．