Question

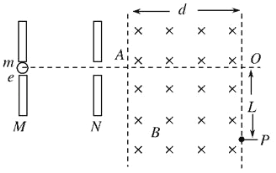
【题目】电子自静止开始经M、N板间（两板间的电压为U）的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中，电子离开磁场时的位置P偏离入射方向的距离为L，如图所示（已知电子的质量为m，电荷量为e）求：

(1)电子在加速电场中加速后获得的速度

(2)匀强磁场的磁感应强度

(3)若d=L则电子在磁场中的运动时间。

Answer 1

【答案】

【解析】

根据动能定理求电子在加速电场中加速后获得的速度；根据几何关系求出电子在磁场中的半径，根据洛伦兹力提供向心力求出磁感应强度；由几何关系求出电子在磁场中偏转的圆心角θ，根据T求出电子在磁场中的运动时间；

解：(1)设电子在M、N两板间经电场加速后获得的速度为v，由动能定理得：

解得：

(2)电子进入磁场后做匀速圆周运动，设其半径为r，则：

由几何关系得：

联立解得：

(3) 由几何关系得：

电子在磁场的周期为：

由几何关系得：

可得电子在磁场中的运动时间：