题目内容
如图所示，正方形线圈原来静止在匀强磁场中，ab边与磁场的边界线重合，线圈面与磁场方向垂直．第一次用时间t把线圈匀速向左从磁场中拉出，在此过程中外力做功W1，通过导线横截面被迁移的电荷量为q1．
第二次用时间t把线圈以ab边为轴匀速转过90°离开磁场，外力做功W2，线圈中被迁移的电荷量为q2．则Wl：W2=
8：π2
8：π2
，q1：q2=1：1
1：1
．分析：第一次：根据E=BLv、欧姆定律、安培力公式得到安培力的一般表达式，根据功的公式求解外力做功，由电量公式q=It求q1；
第二次线圈中产生正弦式电流，由Em=BSω求出感应电动最大值，由E=
Em求出有效值，根据功能关系求外力做功．根据q=
=
，求q2；
第二次线圈中产生正弦式电流，由Em=BSω求出感应电动最大值，由E=
| ||
| 2 |
| △Φ |
| R |
| BL2 |
| R |
解答：解：设正方形的边长为L．
第一次：线圈产生的感应电动势为 E=BLv，感应电流为 I=
，所受的安培力大小为 FA=BIL=
由于线圈匀速运动，则外力F外=FA=
，外力做功W1=F外L=
?L=
=
；通过导线横截面被迁移的电荷量为q1=It=
=
．
第二次：线圈产生的感应电动势最大值为Em=BSω=BL2?
=
有效值为 E=
Em=
?
=
外力做功W2=
t=
t=
线圈中被迁移的电荷量为q2=
=
故Wl：W2=8：π2；q1：q2=1：1．
故答案为：8：π2、1：1
第一次：线圈产生的感应电动势为 E=BLv，感应电流为 I=
| E |
| R |
| B2L2v |
| R |
由于线圈匀速运动，则外力F外=FA=
| B2L2v |
| R |
| B2L2v |
| R |
B2L3
| ||
| R |
| B2L4 |
| tR |
| BLvt |
| R |
| BL2 |
| R |
第二次：线圈产生的感应电动势最大值为Em=BSω=BL2?
| ||
| t |
| BL2π |
| 2t |
有效值为 E=
| ||
| 2 |
| ||
| 2 |
| BL2π |
| 2t |
| ||
| 4t |
外力做功W2=
| E2 |
| R |
(
| ||||
| R |
| B2L4π2 |
| 8tR |
线圈中被迁移的电荷量为q2=
| △Φ |
| R |
| BL2 |
| R |
故Wl：W2=8：π2；q1：q2=1：1．
故答案为：8：π2、1：1
点评：本题掌握法拉第电磁感应定律、欧姆定律、电量公式、安培力公式是基础，关键要注意第二次产生的是正弦式电流，要用有效值求外力做功．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图所示一正方形线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动，沿着OO′观察，线圈沿逆时针方向转动．已知匀强磁场的磁感应强度为B，线圈匝数为n，边长为l，电阻为R，转动的角速度为ω．则当线圈转至图示位置时（ ）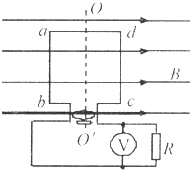
如图所示，正方形线圈abcd谢绕对称轴OO′在匀强磁场中匀速转动，转速为
（2008?武汉二模）如图所示，正方形线圈abcd位于纸面内，边长为L，匝数为N，过ab中点和cd中点的连线OO′恰好位于垂直纸面向里的匀强磁场的右边界上，磁感应强度为B，则穿过线圈的磁通量为（ ）
