题目内容
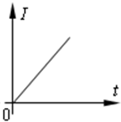
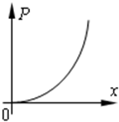
如图所示，在竖直方向的磁感应强度为B的匀强磁场中，金属框架ABCD（框架电阻忽略不计）固定在水平面内，AB与CD平行且足够长，BC与CD夹角θ（θ＜90°），光滑均匀导体棒EF（垂直于CD）紧贴框架，在外力作用下以垂直于自身的速度v向右匀速运动，经过C点作为计时起 点，下列关于电路中电流大小I与时间t、消耗的电功率P与导体棒水平移动的距离x变化规律的图象中正确的是（ ）分析：金属棒从C运动到B的过程中，有效切割长度在不断的增大，根据几何关系写出有效长度的表达式，然后根据法拉第电磁感应定律求解即可，当金属棒通过B点之后有效切割长度不变，因此电动势、电流、功率等不发生变化，因此正确解答本题的关键是弄清导线在从C运动到B过程中的电动势、电流、功率等变化情况．
解答：解：A、设金属棒的速度为v，则运动过程中有效切割长度为：L=vt×tanθ
设金属棒横截面积为s，电阻率为ρ，则回路中电阻为：R=ρ
．
所以回路中的电流为：I=
=
，为定值．故A、B错误．
C、设导体棒在到达B之前运动的距离为x，则有：
电动势为：E=BLv=Bxtanθv
电阻为：R=ρ
功率为：P=
=
，故开始功率随着距离增大而均匀增大，当通过B点之后，感应电动势不变，回路中电阻不变，故功率不变，故D正确，C错误．
故选D．
设金属棒横截面积为s，电阻率为ρ，则回路中电阻为：R=ρ
| vt×tanθ |
| s |
所以回路中的电流为：I=
| BLv |
| R |
| Bvs |
| ρ |
C、设导体棒在到达B之前运动的距离为x，则有：
电动势为：E=BLv=Bxtanθv
电阻为：R=ρ
| xtanθ |
| s |
功率为：P=
| E2 |
| R |
| B2v2stanθx |
| ρ |
故选D．
点评：对于这类问题不能盲目凭感觉进行判断，要根据数学关系和所学物理规律求出物理量之间的表达式进行判断，否则容易出错．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，在竖直方向的磁感应强度为B的匀强磁场中，金属框架ABCD（框架电阻忽略不计）固定在水平面内，AB与CD平行且足够长，BC与CD夹角θ（θ＜90°），光滑均匀导体棒EF（垂直于CD）在外力作用下以垂直于自身的速度v向右匀速运动，导体棒在滑动过程中始终保持与框架良好接触，经过C点瞬间作为计时起点，下列关于电路中电流大小I与时间t、消耗的电功率P与导体棒水平移动的距离x变化规律的图象中正确的是（ ）
如图所示是在竖直方向上振动并沿水平方向传播的简谐波，实线是t=0s时刻的波形图，虚线是t=0.2s时刻的波形图．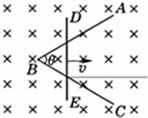
如图所示，在竖直方向的磁感应强度为B的匀强磁场中，金属框架ABC固定在水平面内，AB与BC间夹角为θ，光滑导体棒DE在框架上从B点开始在外力作用下以速度v向右匀速运动，导体棒与框架足够长且构成等腰三角形电路．若框架与导体棒单位长度的电阻均为R，导体棒在滑动过程中始终保持与导轨良好接触，下列关于电路中电流大小I与时间t、消耗的电功率P与水平移动的距离x变化规律的图象中正确的是（ ）
