题目内容
如图所示，一根光滑的轻杆沿水平方向放置，左端O处连接在竖直的转动轴上，a、b为两个可看做质点的小球，穿在杆上，并用细线分别连接Oa和ab，且Oa=ab，已知b球质量为a球质量的2倍．当轻杆绕O轴在水平面内匀速转动时，Oa和ab两线的拉力之比F1：F2 为（ ）分析：a球在水平方向上受oa、ab的拉力，靠两个力的拉力提供向心力，b球在水平方向上受ab的拉力，靠该拉力提供向心力，抓住两球角速度相等，根据牛顿第二定律求出Oa和ab两线的拉力之比．
解答：解：对a球有：F1-F2=mroaω2，对b球有：F2=2m?robω2，因为rob=2roa，所以
=4，解得
=
．故D正确，A、B、C错误．
故选D．
| F2 |
| F1-F2 |
| F1 |
| F2 |
| 5 |
| 4 |
故选D．
点评：解决本题的关键确定物体做圆周运动向心力的来源，运用牛顿第二定律进行求解．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
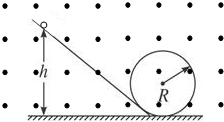如图所示，一根光滑的绝缘斜槽连接一个竖放置的半径为R=0.50m的圆形绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T．有一个质量m=0.10g，带电量为q=+1.6×10-3C的小球在斜轨道上某位置由静止自由下滑，若小球恰好能通过最高点，则下列说法中正确的是（重力加速度取10m/s2）
如图所示，一根光滑的绝缘斜槽连接一个竖放置的半径为R=0.50m的圆形绝缘光滑槽轨．槽轨处在垂直纸面向外的匀强磁场中，磁感应强度B=0.50T．有一个质量m=0.10g，带电量为q=+1.6×10-3C的小球在斜轨道上某位置由静止自由下滑，若小球恰好能通过最高点，则下列说法中正确的是（重力加速度取10m/s2）（ ）
O点自由释放。设小球、杆和地球系统的机械能为E，球、杆绕过O点的
B．E不变，L不变
成立
m