题目内容
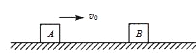
【题目】如图所示,质量为m1=0.2kg小物块A沿水平面与小物块B发生正碰,小物块B的质量m2=1.0kg。已知碰撞前A的速度大小为v0=3.0 m/s,B静止在水平面上,两物块与水平面间的动摩擦因数均为μ=0.2,重力加速度g取10m/s2。试求碰后物块B在水平面上滑行的时间。
【答案】0.25 s≤t≤0.5 s
【解析】假如两物块发生的是完全非弹性碰撞,碰后的共同速度为v1,则由动量守恒定律有:
m1v0=(m1+m2)v1
碰后,A、B一起滑行直至停下,设滑行时间为t1,则由动量定理有:
μ(m1+m2)gt1=(m1+m2)v1
解得t1=0.25 s
假如两物块发生的是弹性碰撞,碰后A、B的速度分别为vA、vB,则由动量守恒定律有:
m1v0=m1vA+m2vB
![]() m1v02=
m1v02=![]() m1vA2+
m1vA2+![]() m2vB2
m2vB2
设碰后B滑行的时间为t2,则:μm2gt2=m2vB
解得t2=0.5 s
可见,碰后B在水平面上滑行的时间t满足: 0.25 s≤t≤0.5 s

练习册系列答案
相关题目