题目内容
如图所示,n块相同的木块,每块质量都是m,大小可忽略,放置在倾角为(1)整个过程中由于碰撞而损失的总机械能;
(2)若n=6,

(共20分) 解析:(1)取n个木块系统为研究对象,对于整个过程,由动能定理得: 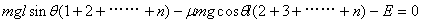 (4分) 所以
(4分) 所以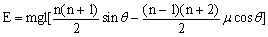 (4分) (2)第1块从开始下滑到与第2块碰撞前
(4分) (2)第1块从开始下滑到与第2块碰撞前 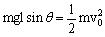 ,得
,得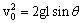 第1块与第2块碰撞过程:
第1块与第2块碰撞过程: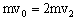
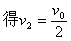 (2分) 第1、2块一起下滑l,由动能定理:
(2分) 第1、2块一起下滑l,由动能定理: 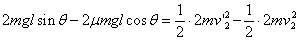 所以
所以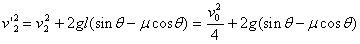 (2分) 第1、2块与第3块碰撞过程
(2分) 第1、2块与第3块碰撞过程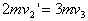 得
得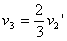 第1、2、3块一起下滑l,由动能定理:
第1、2、3块一起下滑l,由动能定理: 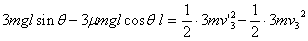 所以
所以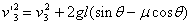
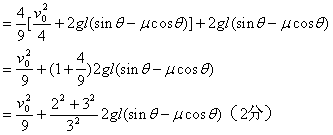 则n块木块一起下滑l的末速度为:
则n块木块一起下滑l的末速度为: 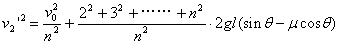 (3分) 由已知条件
(3分) 由已知条件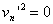 当n=6,
当n=6,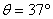 时,
时,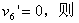
 即
即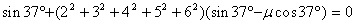
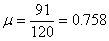 (3分)
(3分)
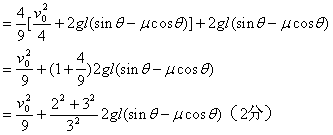 则n块木块一起下滑l的末速度为:
则n块木块一起下滑l的末速度为: 
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
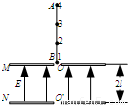
 (2009?广州二模)如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求:
(2009?广州二模)如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板间距离为2L,两板间存在竖直向上的匀强电场.AB是一长3L的轻质绝缘细杆,杆上等间距地固定着四个完全相同的带电小球(1、2、3、4),每个小球的电荷量为q、质量为m,相邻小球间的距离为L.第一个小球置于孔O处,将AB由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场这一过程中AB杆一直做匀速直线运动,且杆保持竖直.求: