题目内容
13.如图所示,某人水平离开平台边缘A点时的速度vA=4.0m/s,恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,并沿轨道滑行.C为轨道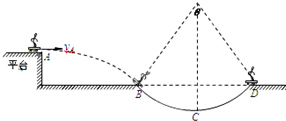 的最低点,B、D为轨道与水平地面的连接点.已知人与滑板可视为质点,其总质量m=60.0kg,滑板与水平地面间的动摩擦因数为μ=0.1,空气阻力忽略不计,轨道半径R=2.0m,轨道BCD对应的圆心角θ=74°,g取10m/s2,cos37°=0.8,sin37°=0.6.
的最低点,B、D为轨道与水平地面的连接点.已知人与滑板可视为质点,其总质量m=60.0kg,滑板与水平地面间的动摩擦因数为μ=0.1,空气阻力忽略不计,轨道半径R=2.0m,轨道BCD对应的圆心角θ=74°,g取10m/s2,cos37°=0.8,sin37°=0.6. (1)求人与滑板在B点的速度大小;
(2)求运动到圆弧最低点C时轨道对人支持力的大小.
分析 (1)人和滑板恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,说明在B点的速度沿B点的切线方向,由几何关系求解在B点的速度大小.
(2)人和滑板在光滑圆弧的运动过程中,只有重力做功,由机械能守恒求得C点速度,再根据牛顿第二定律求支持力.
解答 解:(1)据题,人和滑板恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,由几何关系得知此时人的速度方向与水平夹角α=37°.
则人与滑板在B点的速度大小 vB=$\frac{{v}_{0}}{cosα}$=$\frac{4}{cos37°}$=5m/s
(2)人和滑板在光滑圆弧的运动过程中,只有重力做功,机械能守恒.则
mgR(1-cos37°)+$\frac{1}{2}$mvB2=$\frac{1}{2}$mvC2
在C点,由牛顿第二定律得:FN-mg=m$\frac{{v}_{C}^{2}}{R}$
解得 FN=1590N
答:
(1)人与滑板在B点的速度大小是5m/s;
(2)运动到圆弧最低点C时轨道对人支持力的大小为1590N.
点评 解决本题的关键抓住无碰撞地从B点进入圆轨道,得出速度的方向.知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.以及知道知道在圆弧轨道的最低点,沿半径方向上的合力提供圆周运动的向心力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.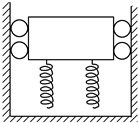 如图所示,一升降机在箱底装有若干弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )
如图所示,一升降机在箱底装有若干弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )
 如图所示,一升降机在箱底装有若干弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )
如图所示,一升降机在箱底装有若干弹簧,设在某次事故中,升降机吊索在空中断裂,忽略摩擦力,则升降机在从弹簧下端触地后直到最低点的一段运动过程中( )| A. | 升降机的速度不断减小 | |
| B. | 升降机的加速度不断变大 | |
| C. | 升降机的加速度最大值等于重力加速度值 | |
| D. | 升降机的加速度最大值大于重力加速度值 |
4.物体做简谐运动过程中,下列说法正确的是( )
| A. | 当振动物体的位移减小时,其速度和加速度的方向必定同向 | |
| B. | 当物体的速度变化最快时,其动能最大 | |
| C. | 当加速度与速度反向时,其回复力正在减小 | |
| D. | 物体的动能相等的两个时刻,其加速度也相同 |
1.从竖直上升的气球上掉下的石块与同一高度自由下落的石块相比,不计石块的空气阻力和浮力,下列各物理量中相等的是( )
| A. | 落地的时间 | B. | 落地时的速度 | C. | 落地时的速率 | D. | 在空中的加速度 |
8. 用三合板模拟拱形桥来研究汽车通过桥的最高点时对桥的压力.在拱桥上表面事先铺上一层牛仔布以增加摩擦,这样玩具车就可以在桥面上跑起来了.把这套系统放在电子秤上,关于电子秤的示数下列说法正确的是( )
用三合板模拟拱形桥来研究汽车通过桥的最高点时对桥的压力.在拱桥上表面事先铺上一层牛仔布以增加摩擦,这样玩具车就可以在桥面上跑起来了.把这套系统放在电子秤上,关于电子秤的示数下列说法正确的是( )
 用三合板模拟拱形桥来研究汽车通过桥的最高点时对桥的压力.在拱桥上表面事先铺上一层牛仔布以增加摩擦,这样玩具车就可以在桥面上跑起来了.把这套系统放在电子秤上,关于电子秤的示数下列说法正确的是( )
用三合板模拟拱形桥来研究汽车通过桥的最高点时对桥的压力.在拱桥上表面事先铺上一层牛仔布以增加摩擦,这样玩具车就可以在桥面上跑起来了.把这套系统放在电子秤上,关于电子秤的示数下列说法正确的是( )| A. | 玩具车静止在拱桥顶端时电子称示数小一些 | |
| B. | 玩具车运动通过拱桥顶端时电子称示数大一些 | |
| C. | 玩具车运动通过拱桥顶端时处于超重状态 | |
| D. | 玩具车运动通过拱桥顶端时速度越大(未离开拱桥),电子称示数越小 |
18.用手握住一个瓶子使其在空中保持竖直且静止,下列说法正确的是( )
| A. | 瓶子越重,瓶子所受的摩擦力越大 | |
| B. | 手越粗糙,瓶子所受的摩擦力越大 | |
| C. | 手的握力越大,瓶子所受的摩擦力越大 | |
| D. | 瓶子所受的摩擦力与瓶子所受重力是一对作用力与反作用力 |
5.下列说法中正确的是( )
| A. | 一定量气体膨胀对外做功100J,同时从外界吸收120J的热量,则它的内能增大20J | |
| B. | 在使两个分子间的距离由很远(r>10-9m)减小到很难再靠近的过程中,分子间作用力先减小后增大,分子势能不断增大 | |
| C. | 由于液体表面层分子间距离大于液体内部分子间距离,液体表面存在张力 | |
| D. | 空气相对湿度越大时,空气中水蒸气压强越接近同温度水的饱和汽压,水蒸发越慢 |
2.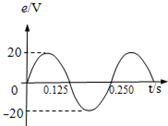 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路.不计电路的其他电阻,下列说法正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路.不计电路的其他电阻,下列说法正确的是( )
 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路.不计电路的其他电阻,下列说法正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路.不计电路的其他电阻,下列说法正确的是( )| A. | t=0.125s 时线圈的磁通量变化率最大 | |
| B. | 交变电流的频率为4Hz | |
| C. | 交变电流的有效值为$\sqrt{2}$A | |
| D. | 交变电流的最大值为4A |
3.甲、乙两个质点同时出发做直线运动,其s-t图象如图所示.下列说法正确的是( )
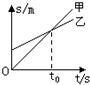

| A. | 甲的速度比乙的大 | B. | 甲的加速度比乙的大 | ||
| C. | t0时刻,甲和乙的速度相等 | D. | 0~t0时间内,甲在乙的前面 |