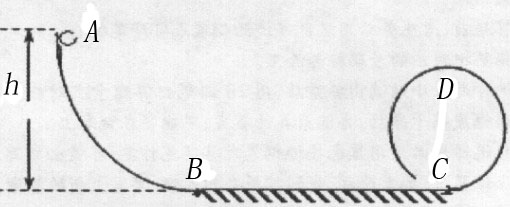
题目内容
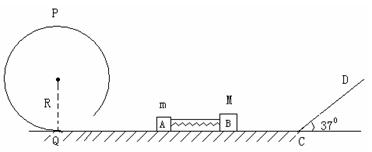
如图所示,质量分别为m和M的滑块A和B静止于光滑的水平台面上,A和B之间夹有一轻质弹簧(A、B与弹簧不连接),弹簧处于被压缩状态,有一轻质绳连接着A和B。水平台面左端连接着一半径为R=0.2m的光滑圆轨道PQ,右端为一倾角为37°的足够长的斜面CD,滑块B与斜面CD间的动摩擦因数为 。烧断两滑块间的轻质绳后,由于弹簧弹力的作用,滑块A将沿圆轨道做圆周运动,且在最高点P轨道对滑块的压力恰好等于滑块的重力。已知两滑块的质量之比为
。烧断两滑块间的轻质绳后,由于弹簧弹力的作用,滑块A将沿圆轨道做圆周运动,且在最高点P轨道对滑块的压力恰好等于滑块的重力。已知两滑块的质量之比为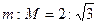 ,重力加速度g=10m/s2.求:
,重力加速度g=10m/s2.求:
(1)烧断细绳,弹簧恢复原长时两滑块的速度大小;
(2)滑块B将沿斜面上滑,且从斜面底端C开始经过t=0.5s,恰好经过D点,求CD的长度。
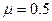 。烧断两滑块间的轻质绳后,由于弹簧弹力的作用,滑块A将沿圆轨道做圆周运动,且在最高点P轨道对滑块的压力恰好等于滑块的重力。已知两滑块的质量之比为
。烧断两滑块间的轻质绳后,由于弹簧弹力的作用,滑块A将沿圆轨道做圆周运动,且在最高点P轨道对滑块的压力恰好等于滑块的重力。已知两滑块的质量之比为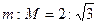 ,重力加速度g=10m/s2.求:
,重力加速度g=10m/s2.求:(1)烧断细绳,弹簧恢复原长时两滑块的速度大小;
(2)滑块B将沿斜面上滑,且从斜面底端C开始经过t=0.5s,恰好经过D点,求CD的长度。

(1)
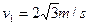 ,
,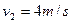 (2)
(2)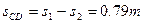
(1)设弹簧恢复原长时A、B两滑块的速率分别为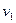 和
和 ,滑块A到达圆轨道最高点时的速率为
,滑块A到达圆轨道最高点时的速率为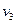
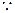 滑块A在最高点,轨道对其的压力恰好与其重力相等
滑块A在最高点,轨道对其的压力恰好与其重力相等
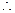
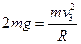 ① (2分)
① (2分)
滑块A在光滑圆轨道上运动过程中机械能守恒,所以有
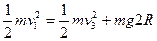 ② (2分)
② (2分)
烧断细绳后,A、B两滑块在弹簧弹力作用下运动过程中动量守恒,且二者运动速度方向相反,所以有:
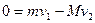 ③ (2分)
③ (2分)
由题给条件有:
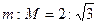 ④ (1分)
④ (1分)
联立以上各式求解得: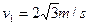 ,
,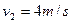 (3分)
(3分)
(2)滑块B在C点时的速度: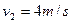
滑块沿CD段向上运动时做匀减速度直线运动至静止,设其加速度大小为 ,发生的位移大小为
,发生的位移大小为 ,所用时间为
,所用时间为 ,则有
,则有
 ⑤ (1分)
⑤ (1分)
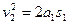 ⑥ (1分)
⑥ (1分)
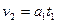 ⑦ (1分)
⑦ (1分)
联立以上三式求解得: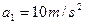 ,
,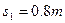 ,
,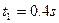 (1分)
(1分)
返回时做初速度为零的匀加速直线运动,设其加速度大小为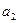 ,运动时间为
,运动时间为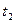 ,位移为
,位移为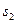 ,则有
,则有
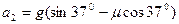 ⑧ (1分)
⑧ (1分)
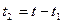 ⑨ (1分)
⑨ (1分)
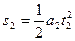 ⑩ (1分)
⑩ (1分)
联立以上三式代数求解得: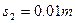 (1分)
(1分)
所有CD的长度为: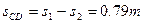 (1分)
(1分)
说明:用其它方法计算,只要正确,同样给分
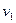 和
和 ,滑块A到达圆轨道最高点时的速率为
,滑块A到达圆轨道最高点时的速率为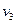
 滑块A在最高点,轨道对其的压力恰好与其重力相等
滑块A在最高点,轨道对其的压力恰好与其重力相等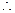
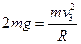 ① (2分)
① (2分)滑块A在光滑圆轨道上运动过程中机械能守恒,所以有
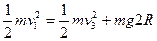 ② (2分)
② (2分)烧断细绳后,A、B两滑块在弹簧弹力作用下运动过程中动量守恒,且二者运动速度方向相反,所以有:
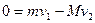 ③ (2分)
③ (2分)由题给条件有:
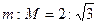 ④ (1分)
④ (1分)联立以上各式求解得:
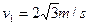 ,
,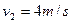 (3分)
(3分)(2)滑块B在C点时的速度:
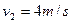
滑块沿CD段向上运动时做匀减速度直线运动至静止,设其加速度大小为
 ,发生的位移大小为
,发生的位移大小为 ,所用时间为
,所用时间为 ,则有
,则有 ⑤ (1分)
⑤ (1分)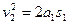 ⑥ (1分)
⑥ (1分)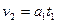 ⑦ (1分)
⑦ (1分)联立以上三式求解得:
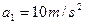 ,
,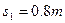 ,
,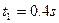 (1分)
(1分)返回时做初速度为零的匀加速直线运动,设其加速度大小为
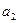 ,运动时间为
,运动时间为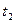 ,位移为
,位移为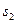 ,则有
,则有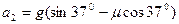 ⑧ (1分)
⑧ (1分)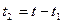 ⑨ (1分)
⑨ (1分)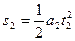 ⑩ (1分)
⑩ (1分)联立以上三式代数求解得:
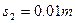 (1分)
(1分) 所有CD的长度为:
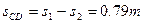 (1分)
(1分)说明:用其它方法计算,只要正确,同样给分

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
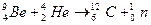
 衰变说明了
衰变说明了 ①A与地面间的动摩擦因数。
①A与地面间的动摩擦因数。
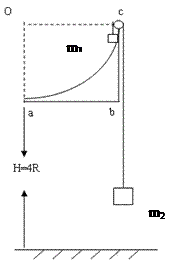
 ,其余各处的摩擦不计,A、B、C均可视为质点,重力加速度为g.
,其余各处的摩擦不计,A、B、C均可视为质点,重力加速度为g.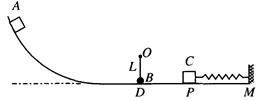
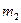 的左端,右端与小木块
的左端,右端与小木块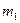 连接,且
连接,且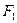 和
和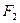 ,从两物体开始运动以后的整个过程中,对
,从两物体开始运动以后的整个过程中,对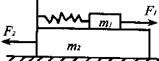

 =0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求:
=0.25,BC长度为L=1m,圆形轨道半径为r=0.1m,g取l0m/s2,求: