��Ŀ����
����Ŀ����ͼ��ʾ��A��B������������ֱ�Ϊ2m��m����ֹ������ˮƽ�����ϣ�A��B��Ķ�Ħ������Ϊ�̣�B������Ķ�Ħ������Ϊ ![]() �̣����Ħ�������ڻ���Ħ�������������ٶ�Ϊg���ֶ�Aʩ��һˮƽ����F���� ��
�̣����Ħ�������ڻ���Ħ�������������ٶ�Ϊg���ֶ�Aʩ��һˮƽ����F���� ��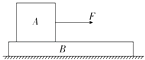
A.��F��2��mgʱ��A��B����Ե��澲ֹ
B.��F= ![]() ��mgʱ��A�ļ��ٶ�Ϊ
��mgʱ��A�ļ��ٶ�Ϊ ![]() ��g
��g
C.��F��3��mgʱ��A���B����
D.����FΪ��ֵ��B�ļ��ٶȲ��ᳬ�� ![]() ��g
��g
���𰸡�B,C,D
���������⣺AB֮������Ħ����Ϊ��fmax=��mAg=2��mg��B����������Ħ����Ϊ��f��max= ![]() �̣�mA+mB��g=1.5��mg��
�̣�mA+mB��g=1.5��mg��
A���� 1.5��mg��F��2��mg ʱ��f��max��F��fmax��AB֮�䲻�ᷢ����Ի�����������������B����������Ħ��������AB�����䷢����Ի�������A����
B����F= ![]() ��mgʱ����A��B��Ȼû������˶�����
��mgʱ����A��B��Ȼû������˶����� ![]()
�֣�F��f��max=��mA+mB��a1
���ԣ� ![]()
��ʱA��B֮���Ħ����f����
mAa1=F��f
���ԣ�f= ![]() ��fmax����֪���������A�ļ��ٶ�Ϊ
��fmax����֪���������A�ļ��ٶ�Ϊ ![]() ��g����B��ȷ��
��g����B��ȷ��
C����F=3��mgʱ����A��B��Ȼû������˶�����F��f��max=3��mg��1.5��mg=1.5��mg
�֣�F��f��max=��mA+mB��a2
���ԣ�a2=0.5��g
��ʱA��B֮���Ħ����f�䣬��
mAa2=F��f��
���ԣ�f��=2��mg=fmax
���Ե�F��3��mgʱ��A���B��������C��ȷ��
D����A��B֮���Ħ�������ʱ��B�ļ��ٶ����ʱB��ˮƽ�����ܵ�����Ħ���������ã���ţ�ٵڶ����ɵã�
mBa3=fmax��f��max=2��mg��1.5��mg=0.5��mg
���ԣ�a3=0.5��g
������FΪ��ֵ��B�ļ��ٶȲ��ᳬ�� ![]() ��g����D��ȷ��
��g����D��ȷ��
��ѡ��BCD
����A��B֮������Ħ�����������B�������������ٽ���ٶȣ�ͨ��ţ�ٵڶ��������A��B��������Ի���ʱ�����������Ȼ��ͨ�����巨���뷨���������