题目内容
18. 如图所示,一根跨过一固定水平光滑细杆O的轻绳,两端各系一小球,球a置于地面,球b被拉到与细杆等高的位置,在绳刚被拉直时(无张力)释放b球,使b球由静止下摆,设两球质量相等,则a球刚要离开地面时,跨越细杆的两段绳之间的夹角为多少?
如图所示,一根跨过一固定水平光滑细杆O的轻绳,两端各系一小球,球a置于地面,球b被拉到与细杆等高的位置,在绳刚被拉直时(无张力)释放b球,使b球由静止下摆,设两球质量相等,则a球刚要离开地面时,跨越细杆的两段绳之间的夹角为多少?
分析 a球刚要离开地面时绳的拉力恰好等于a的重力.由动能定理得出b球的速度,由牛顿第二定律得出绳子的拉力与速度的关系,联立可解得两段绳之间的夹角.
解答  解:设a球刚要离开地面时,两段绳间夹角为θ,此时b的速度为v,a、b球质量均为m,则在b球摆下过程中,根据动能定理得
解:设a球刚要离开地面时,两段绳间夹角为θ,此时b的速度为v,a、b球质量均为m,则在b球摆下过程中,根据动能定理得
mglcosθ=$\frac{1}{2}m{v}^{2}$ ①
则得 mv2=2mglcosθ ②
b摆到C点时,根据牛顿第二定律得:
F-mgcosθ=m$\frac{{v}^{2}}{l}$ ③
据题有 F=mg ④
由①②③④式得
cosθ=$\frac{1}{3}$,θ=arccos$\frac{1}{3}$.
答:a球刚要离开地面时,跨越细杆的两段绳之间的夹角为arccos$\frac{1}{3}$.
点评 本题综合考查了动能定理、牛顿第二定律,关键搞清向心力的来源:指向圆心的合力提供向心力,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
8. 如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )
 如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )| A. | 金属块带负电荷 | |
| B. | 电场力做功4 J | |
| C. | 金属块的电势能与动能之和增加了16 J | |
| D. | 金属块的机械能减少12 J |
9. 如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
 如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )| A. | 闭合S1,接通S2的瞬间 | |
| B. | 闭合S1和S2,断开S2的瞬间 | |
| C. | 闭合S1和S2,断开S1的瞬间 | |
| D. | 断开S1,闭合S2,滑动滑动变阻器滑片的过程中 |
13. 如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
 如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )| A. | 在该过程中,物块也做匀速运动 | B. | 人对物块做功$\frac{1}{2}$mv02 | ||
| C. | 人对物块做功$\frac{{m{V_0}^2{S^2}}}{{2({h^2}+{S^2})}}$ | D. | 物块运动的速率为$\frac{{{V_0}h}}{{\sqrt{{h^2}+{S^2}}}}$ |
7. 均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )
均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )
 均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )
均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场.如图所示,在半球面AB上均匀分布正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R,已知M点的场强大小为E,则N点的场强大小为( )| A. | $\frac{kq}{4{R}^{2}}$-E | B. | $\frac{kq}{4{R}^{2}}$+E | C. | $\frac{kq}{2{R}^{2}}$-E | D. | $\frac{kq}{2{R}^{2}}$+E |
8.如图所示,小强正在荡秋千.关于绳上a、b、c点的线速度关系,下列正确的是( )


| A. | va=vb=vc | B. | va>vb>vc | C. | va<vb<vc | D. | va<v c<vb |
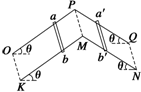 如图所示,两根足够长的“∧”形状的金属导轨构成两个斜面,斜面与水平面间夹角均为θ=37°,导轨间距L=1m,导轨电阻可忽略不计.两根相同的金属棒ab和a′b′的质量都为m=0.2kg,电阻R=1Ω,与导轨垂直放置且接触良好,金属棒和导轨之间的动摩擦因数μ=0.25,两个导轨斜面分别处于垂直于自身斜面向上的两匀强磁场中(图中未画出),磁感应强度B的大小相同.让a′b′在平行于斜面的外力F作用下保持静止,将金属棒ab由静止开始释放,当ab下滑速度达到稳定时,整个回路消耗的电功率为P=8W.g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图所示,两根足够长的“∧”形状的金属导轨构成两个斜面,斜面与水平面间夹角均为θ=37°,导轨间距L=1m,导轨电阻可忽略不计.两根相同的金属棒ab和a′b′的质量都为m=0.2kg,电阻R=1Ω,与导轨垂直放置且接触良好,金属棒和导轨之间的动摩擦因数μ=0.25,两个导轨斜面分别处于垂直于自身斜面向上的两匀强磁场中(图中未画出),磁感应强度B的大小相同.让a′b′在平行于斜面的外力F作用下保持静止,将金属棒ab由静止开始释放,当ab下滑速度达到稳定时,整个回路消耗的电功率为P=8W.g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
