题目内容
在一种叫“蹦极跳”的运动中,质量为m的游戏者身系一根自然长度为L、劲度系数为k的弹性良好的轻质柔软橡皮绳,从高处由静止开始下落1.5L时到达最低点,若在下落过程中不计空气阻力,则下列说法中正确的是
- A.下落高度为L时速度最大,然后速度开始减小,到最低点时速度为零
- B.人在整个下落过程的运动形式为先做匀加速运动,后做匀减速运动
- C.下落高度为L+mg/k时,游戏者速度最大
- D.在到达最低点时,速度、加速度均为零
C
分析:在弹性绳从原长达最低点的过程中,开始阶段,游戏者的重力大于橡皮绳的拉力,游戏者做加速运动,后来橡皮绳的拉力大于游戏者的重力,游戏者做减速运动,根据牛顿第二定律分析加速度变化情况.
解答:A、游戏者先做自由落体运动,在弹性绳从原长达最低点的过程中,开始阶段,游戏者的重力大于橡皮绳的拉力,根据牛顿第二定律,加速度方向向下,先向下做加速度减小的加速运动,当弹力和重力相等时,速度达到最大,然后橡皮绳的拉力大于游戏者的重力,加速度方向向上,做加速度逐渐增大的减速运动,到达最低点时,速度为零,加速度达到最大.故A、B、D错误.
C、当弹力和重力相等时,速度最大,根据胡克定律有mg=kx,x=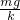 ,游戏者下落的高度h=
,游戏者下落的高度h= .故C正确.
.故C正确.
故选C.
点评:解决本题的关键会根据牛顿第二定律判断加速度的变化,会根据速度方向和加速度方向的关系判断速度的变化.
分析:在弹性绳从原长达最低点的过程中,开始阶段,游戏者的重力大于橡皮绳的拉力,游戏者做加速运动,后来橡皮绳的拉力大于游戏者的重力,游戏者做减速运动,根据牛顿第二定律分析加速度变化情况.
解答:A、游戏者先做自由落体运动,在弹性绳从原长达最低点的过程中,开始阶段,游戏者的重力大于橡皮绳的拉力,根据牛顿第二定律,加速度方向向下,先向下做加速度减小的加速运动,当弹力和重力相等时,速度达到最大,然后橡皮绳的拉力大于游戏者的重力,加速度方向向上,做加速度逐渐增大的减速运动,到达最低点时,速度为零,加速度达到最大.故A、B、D错误.
C、当弹力和重力相等时,速度最大,根据胡克定律有mg=kx,x=
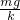 ,游戏者下落的高度h=
,游戏者下落的高度h= .故C正确.
.故C正确.故选C.
点评:解决本题的关键会根据牛顿第二定律判断加速度的变化,会根据速度方向和加速度方向的关系判断速度的变化.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目