题目内容
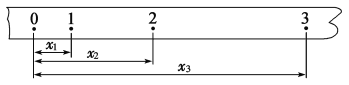
【题目】玻璃砖的截面为等腰三角形ABC,如图所示,底边BC=a,∠A=30°,图中的虚线为底边BC的垂直平分线,且垂足为O.一细光束由O点斜射入玻璃砖内,当该细光束第一次射到AB边时,刚好发生全反射,已知该玻璃砖对该光的折射率为n=![]() ,光在真空中的传播速度用c表示
,光在真空中的传播速度用c表示
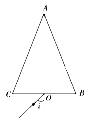


(i)求细光束在底边BC的入射角i;
(ii)求该细光束从O点射入玻璃砖到第一次射到AB边所需的时间.
【答案】(i) i=45°;(ii) t=a
【解析】
(i)根据细光束第一次射到AB边时刚好发生全反射可知,细光束在AB边上的入射角等于全反射临界角αC,由折射定律得sin αC=1/n


代入数据解得αC=45°
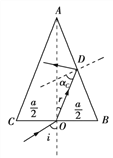
设细光束在BC边的折射角大小为r,由几何关系可得r=30°
根据折射定律得![]()
代入数据解得i=45°
(ii)对△OBD由正弦定理: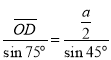
假设细光束从O点射入玻璃砖到第一次射到AB边所需的时间为t,细光束在玻璃砖中的速度为![]()
又由![]()
联立解得t=a

 名校课堂系列答案
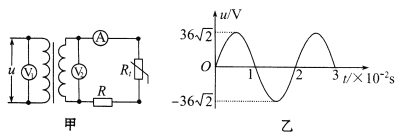
名校课堂系列答案【题目】橡皮筋在弹性限度内,其伸长量x与所受到的拉力F成正比,即F=kx,其中k为橡皮筋的劲度系数,某物理实验小组利用如图甲所示的实验装置测量橡皮筋的劲度系数,实验步骤如下:

a.将橡皮筋上端固定,使其自然下垂,测出此时橡皮筋的长度L0;
b.在橡皮筋的下端分别挂1个钩码、2个钩码、3个钩码、…,对应的橡皮筋的长度分别记为L1、L2、L3、…
该实验小组测量的数据如下表所示:(每个钩码的质量为50 g,重力加速度g取9.8 m/s2)
钩码个数n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
橡皮筋长度L/cm | 20.00 | 22.40 | 24.85 | 27.35 | 29.83 | 32.18 | 34.65 | 37.15 |
(1)为了充分利用数据,该小组将测量的数据逐一求差,d1=L4-L0=9.83 cm,d2=L5-L1=9.78 cm,d3=L6-L2=9.80 cm,d4=L7-L3=9.80 cm。根据所得的差值,可以计算出每增加一个钩码时橡皮筋的平均伸长量![]() ,则
,则![]() 用d1、d2、d3、d4可表示为
用d1、d2、d3、d4可表示为![]() =____;由此计算出橡皮筋的劲度系数k=____N/m。
=____;由此计算出橡皮筋的劲度系数k=____N/m。
(2)该小组进一步查阅资料发现,杨氏弹性模量Y也是表征固体材料性质的一个重要物理量。已知固体材料所受到的拉力F与其截面积S之比称为该固体材料的应力,固体材料的伸长量x与其原长L0之比称为该固体材料的应变,应力与应变的比值称为该材料的杨氏弹性模量。根据胡克定律和杨氏弹性模量的定义,可得出杨氏弹性模量Y与劲度系数k之间的关系式为Y=____。
(3)若该小组在实验中使用的是横截面为圆形的橡皮筋,用螺旋测微器测得的橡皮筋横截面的直径d如图乙所示,则d=____mm。