题目内容
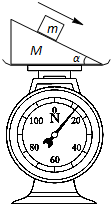（2012?虹口区二模）如图所示，倾角为α、质量为M的斜面体放在一架台秤上，小滑块的质量为m．若滑块、斜面体均处于静止状态，则台秤的读数为（m+M）g
（m+M）g
；若滑块以加速度a沿斜面体加速下滑，而斜面体仍然保持静止，则台秤的读数为（m+M）g-masinα
（m+M）g-masinα
．分析：第一种情况下根据平衡条件得到台秤受到的压力；第二种情况根据牛顿第二定律列式求解即可．
解答：解：滑块、斜面体均处于静止状态时，台秤读数等于总重力，即（M+m）g；
滑块以加速度a沿斜面体加速下滑时，对滑块和斜面体整体受力分析，受总重力、支持力和台秤对其向右的静摩擦力f，将滑块的加速度沿着水平和竖直方向正交分解，根据牛顿第二定律，有
水平方向：f=m?acosα
竖直方向：（M+m）g-FN=m?asinα
解得
FN=（M+m）g-masinα
故答案为：（m+M）g，（m+M）g-masinα．
滑块以加速度a沿斜面体加速下滑时，对滑块和斜面体整体受力分析，受总重力、支持力和台秤对其向右的静摩擦力f，将滑块的加速度沿着水平和竖直方向正交分解，根据牛顿第二定律，有
水平方向：f=m?acosα
竖直方向：（M+m）g-FN=m?asinα
解得
FN=（M+m）g-masinα
故答案为：（m+M）g，（m+M）g-masinα．
点评：本题关键对整体受力分析，然后对整体运用牛顿第二定律列式分析求解，由于两物体相对滑动，较难！
练习册系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
（2012?虹口区二模）如图所示，在柱形容器中装有部分水，容器上方有一可自由移动的活塞．容器水面浮有一个木块和一个一端封闭、开口向下的玻璃管，玻璃管中有部分空气，系统稳定时，玻璃管内空气柱在管外水面上方的长度为a，空气柱在管外水面下方的长度为b，水面上方木块的高度为c，水面下方木块的高度为d．现在活塞上方施加竖直向下、且缓缓增大的力F，使活塞下降一小段距离（未碰及玻璃管和木块），下列说法中正确的是（ ）
（2012?虹口区二模）在水平放置的光滑绝缘杆ab上，挂有两个金属环M和N，两环套在一个通电密绕长螺线管的中部，螺线管中部区域的管外磁场可以忽略．当变阻器的滑动头向左移动时，两环的运动情况是（ ）