题目内容
如图所示，质量M = 0.8kg的小车静止在光滑的水平面上，左端紧靠竖直墙．在车上左端水平固定着一只弹簧，弹簧右端放一个质量m = 0.2kg的滑块，弹簧为原长时，滑块位于C处（滑块可以视为质点），车的上表面AC部分为光滑水平面，CB部分为粗糙水平面．CB长l = 1m与滑块的动摩擦因数
=" 0." 4．水平向左推动滑块，将弹簧压缩，然后再把滑块从静止释放，在压缩弹簧过程中推力做功2.5J，滑块释放后将在车上往复运动，最终停在车上某处．设滑块与车的B端碰撞时机械能无损失，g取10m/s2，求：
（1）滑块释放后，第一次离开弹簧时的速度大小；
（2）滑块停在车上的位置离B端多远?
=" 0." 4．水平向左推动滑块，将弹簧压缩，然后再把滑块从静止释放，在压缩弹簧过程中推力做功2.5J，滑块释放后将在车上往复运动，最终停在车上某处．设滑块与车的B端碰撞时机械能无损失，g取10m/s2，求：（1）滑块释放后，第一次离开弹簧时的速度大小；
（2）滑块停在车上的位置离B端多远?
（1）v1=5m/s
（2）距B端0.5m远处
（2）距B端0.5m远处
（1）滑块释放后，弹簧的弹性势能将全部转化为滑块的动能，而弹簧的弹性势能等于推力做的功，所以EP = W =
，代入数值可求得滑块第一次离开弹簧时的速度v1=5m/s；
（2）由于滑块释放后，在与小车（包括弹簧）相对运动的过程中系统动量守恒，且最终两者具有相同的速度，设为v2，则有：mv1= (m + M)v2，
所以系统的最终速度v2=1m/s，对于整个系统来说，总的机械能减少量等于系统内能的增量，
所以E损=mgL=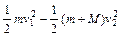
，解得L=2.5m。
由于系统的机械能仅在滑块在BC区间内运动的过程中有损失，且滑块与B端碰后相对于车返回向右运动．可见滑块相对车由C到B，再返回到某一点后，又相对车向右运动，最终停在BC的中点处，即距B端0.5m远处．
，代入数值可求得滑块第一次离开弹簧时的速度v1=5m/s；（2）由于滑块释放后，在与小车（包括弹簧）相对运动的过程中系统动量守恒，且最终两者具有相同的速度，设为v2，则有：mv1= (m + M)v2，
所以系统的最终速度v2=1m/s，对于整个系统来说，总的机械能减少量等于系统内能的增量，
所以E损=
mgL=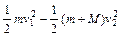，解得L=2.5m。由于系统的机械能仅在滑块在BC区间内运动的过程中有损失，且滑块与B端碰后相对于车返回向右运动．可见滑块相对车由C到B，再返回到某一点后，又相对车向右运动，最终停在BC的中点处，即距B端0.5m远处．
练习册系列答案
相关题目
冲上倾角为θ的粗糙斜面，图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系（以斜面底端为零势能面，
表示上升的最大高度，图中坐标数据中的
为常数且满足
），则由图可知，下列结论正确的是（ ）
时，小球重力势能和动能相等
时，小球重力势能和动能相等
的物体
用绕过定滑轮的细绳与质量为
的物体
相连接，
，开始它们都处于静止状态。现将
.
沿固定斜面由底端向上运动，当它回到出发点时速率为
，且
劲度系数有关
弹性势能
的大小与弹簧自身的长度有关