题目内容
2.已知地球质量为M,万有引力恒量为G,地球半径为R,人造卫星在高空绕地球运行的轨道半径为r,则其绕地球运行的环绕速度V=$\sqrt{\frac{GM}{r}}$,在地球表面附近运行的人造卫星的第一宇宙速度V1=$\sqrt{\frac{GM}{R}}$.分析 第一宇宙速度是卫星在近地圆轨道上的环绕速度,根据引力等于向心力,列式求解;
根据万有引力提供向心力表示出线速度即可求解.
解答 解:高空的物体受到的万有引力提供向心力,由牛顿第二定律,则有:$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
解得:环绕速度也可为:V=$\sqrt{\frac{GM}{r}}$
第一宇宙速度是卫星在近地圆轨道上的环绕速度,
根据引力等于向心力,列式得:$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{\frac{GM}{R}}$
故答案为:$\sqrt{\frac{GM}{r}}$,$\sqrt{\frac{GM}{R}}$.
点评 抓住卫星所受的万有引力等于向心力这个关系即可列式求解!向心力公式根据需要合理选择.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列说法正确的是( )
| A. | 氢原子从高能级向低能级跃迁的过程中释放的光子的能量有可能大于13.6eV | |
| B. | 物质波就是任何一个运动着的物体都有一种波与它对应,该波的波长与该物体的动量成反比 | |
| C. | 在探究光电效应的实验中,若入射光的强度越强,则光电流就越大 | |
| D. | 光在传播过程中主要表现为波动性而在与物体发生相互作用时主要表现为粒子性 |
10.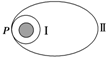 “嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )
“嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )
 “嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )
“嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )| A. | “嫦娥”一号应在P点启动火箭向后喷气 | |
| B. | “嫦娥”一号应在P点启动火箭向前喷气 | |
| C. | “嫦娥”一号在椭圆轨道上运动时,机械能不守恒 | |
| D. | “嫦娥”一号在椭圆轨道上运动的周期与在圆轨道上运动的周期相同 |
17.物体运动过程中,若速度发生变化,则此过程中( )
| A. | 物体动量一定发生变化 | B. | 合外力一定对物体施加冲量 | ||
| C. | 物体动能一定发生变化 | D. | 合外力一定对物体做功 |
7.足球运动员将一只沿水平方向飞来的足球反向踢回的过程中,若足球动量变化量的大小为10kg•m/s,则( )
| A. | 足球的动量一定减小 | B. | 足球的动量一定增大 | ||
| C. | 足球的动量大小可能不变 | D. | 足球的动量大小一定变化 |
11.探月工程三期飞行试验器于2014年10月24日2时在中国西昌卫星发射中心发射升空,飞行试验器飞抵距月球6万千米附近进入月球引力影响区,开始在月球近旁转向飞行,最终进入距月球表面h=200km的圆形工作轨道.设月球半径为R,月球表面的重力加速度为g,万有引力常量为G,则下列选项错误的是( )
| A. | 飞行试验器绕月球运行的周期为2π$\sqrt{\frac{R}{g}}$ | |
| B. | 飞行试验器工作轨道处的重力加速度为($\frac{R}{R+h}$)2g | |
| C. | 飞行试验器在工作轨道上的绕行速度为R$\sqrt{\frac{g}{R+h}}$ | |
| D. | 月球的平均密度为$\frac{3g}{4πGR}$ |

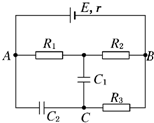 如图所示,电源电动势E=12V,内阻r=1Ω,电阻R1=3Ω,R2=2Ω,R3=5Ω,电容器的电容C1=4 μF,C2=1 μF,求C1、C2所带电荷量.
如图所示,电源电动势E=12V,内阻r=1Ω,电阻R1=3Ω,R2=2Ω,R3=5Ω,电容器的电容C1=4 μF,C2=1 μF,求C1、C2所带电荷量. 一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心,一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,已知真空中的光速为c.sin35°=$\frac{\sqrt{3}}{3}$,求该光线从A点进入透明体到从B点离开透明体所经历的时间.
一底面半径为R的半圆柱形透明体的折射率为n=$\sqrt{3}$,横截面如图所示,O表示半圆柱形截面的圆心,一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,已知真空中的光速为c.sin35°=$\frac{\sqrt{3}}{3}$,求该光线从A点进入透明体到从B点离开透明体所经历的时间.