题目内容
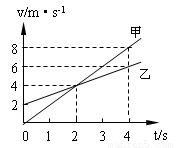
 甲、乙两物体同时同地出发,沿同一方向做匀加速直线运动,它们的v-t图象如图所示.
甲、乙两物体同时同地出发,沿同一方向做匀加速直线运动,它们的v-t图象如图所示.(1)计算甲、乙物体的加速度a甲、a乙
(2)甲、乙两物体何时相遇?相遇时离出发点的距离为多少?
(3)相遇前何时甲、乙相距最远?最远距离为多少?
分析:(1)根据加速度的定义式a=
求解甲、乙两物体的加速度.
(2)甲、乙两物体同时同地出发,沿同一方向做匀加速直线运动,当两物体的位移相等时相遇,根据速度图象的“面积”大小等于位移,由图求出相遇所经历的时间,并由“面积”求出相遇时离出发点的距离.
(3)当两物体速度相等时,相距最远,最远距离等于位移之差,由图读出速度相等的时间,由“面积”求出相距的最远距离.
| △v |
| △t |
(2)甲、乙两物体同时同地出发,沿同一方向做匀加速直线运动,当两物体的位移相等时相遇,根据速度图象的“面积”大小等于位移,由图求出相遇所经历的时间,并由“面积”求出相遇时离出发点的距离.
(3)当两物体速度相等时,相距最远,最远距离等于位移之差,由图读出速度相等的时间,由“面积”求出相距的最远距离.
解答:解:(1)甲的加速度为a甲=
=
m/s2=2m/s2,乙的加速度为a乙=
=
m/s 2=1m/s2.
(2)由题,甲乙两物体同时同地出发,沿同一方向做匀加速直线运动,当位移相等时两物体相遇,根据速度图象的“面积”大小等于位移,可知t=4s时刻两物体相遇,相遇时离出发点的距离为 S=
×8×4m=16m.
(3)在t=2s前,乙的速度大于甲的速度,乙在甲的前方,两者距离增大;t=2s后,乙的速度小于甲的速度,两者距离减小,则知t=2s时,两物体速度相等,相距最远,由图可得:
最远距离等于乙与甲的位移之差,则最远距离为Smax=x乙-x甲=
×2m-
×2×4m=2m.
答:(1)甲的加速度为2m/s2,乙的加速度为1m/s2;
(2)甲乙两物体在t=4s时刻相遇,相遇时离出发点的距离为16m.
(3)相遇前t=2s甲乙相距最远,最远距离为2m.
| △v甲 |
| △t甲 |
| 8-0 |
| 4-0 |
| △v乙 |
| △t乙 |
| 6-2 |
| 4-0 |
(2)由题,甲乙两物体同时同地出发,沿同一方向做匀加速直线运动,当位移相等时两物体相遇,根据速度图象的“面积”大小等于位移,可知t=4s时刻两物体相遇,相遇时离出发点的距离为 S=
| 1 |
| 2 |
(3)在t=2s前,乙的速度大于甲的速度,乙在甲的前方,两者距离增大;t=2s后,乙的速度小于甲的速度,两者距离减小,则知t=2s时,两物体速度相等,相距最远,由图可得:
最远距离等于乙与甲的位移之差,则最远距离为Smax=x乙-x甲=
| 2+4 |
| 2 |
| 1 |
| 2 |
答:(1)甲的加速度为2m/s2,乙的加速度为1m/s2;
(2)甲乙两物体在t=4s时刻相遇,相遇时离出发点的距离为16m.
(3)相遇前t=2s甲乙相距最远,最远距离为2m.
点评:本题根据加速度的定义式求解加速度,通过分析两物体的位移关系和速度关系,判断两物体何时相遇,何时相距最远.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 甲、乙两物体同时同地出发,沿同一方向做匀加速直线运动,它们的v-t图象如图所示.
甲、乙两物体同时同地出发,沿同一方向做匀加速直线运动,它们的v-t图象如图所示.