题目内容
(2012福建南安一中期末).(16分) 如图所示,将一质量m=0.1kg的小球自水平平台顶端O点水平抛出,小球恰好与斜面无碰撞的落到平台右侧一倾角为![]() =53°的光滑斜面顶端A并沿斜面下滑,然后以不变的速率过B点后进入光滑水平轨道BC部分,再进入光滑的竖直圆轨道内侧运动.已知斜面顶端与平台的高度差h=3.2m,斜面顶端高H=15m,竖直圆轨道半径R=5m.(sin530=0.8,cos530=0.6,g=10m/s2). 求:
=53°的光滑斜面顶端A并沿斜面下滑,然后以不变的速率过B点后进入光滑水平轨道BC部分,再进入光滑的竖直圆轨道内侧运动.已知斜面顶端与平台的高度差h=3.2m,斜面顶端高H=15m,竖直圆轨道半径R=5m.(sin530=0.8,cos530=0.6,g=10m/s2). 求:
(1)小球水平抛出的初速度υo及斜面顶端与平台边缘的水平距离x;
(2)小球离开平台后到达斜面底端的速度大小;
(3)小球运动到圆轨道最高点D时轨道对小球的弹力大小.

解析:(1)小球做平抛运动,小球落至A点时,由平抛运动速度分解图可得:
v0=vycotα vA=![]() vy2=2gh
vy2=2gh
h=![]() , x= v0t
, x= v0t
由上式解得:v0=6m/s x=4.8m
vA=10m/s (8分)
(2)由动能定理可得小球到达斜面底端时的速度vB
mgH=![]()
vB=20m/s (3分)


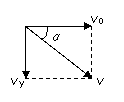

练习册系列答案
相关题目
