题目内容
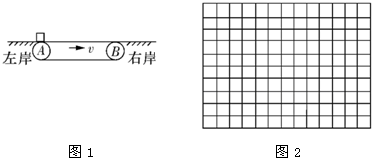
如图1所示为车站、机场使用的水平传送带模型,长为L=3m的水平传送带AB,与左右岸平台位于同一水平面内,设货物(可视为质点)以水平初速度v0=4m/s,从左岸滑上传送带.已知重力加速度g=10m/s2,货物与传送带之间的摩擦因数为0.2,货物与岸的摩擦因数为0.4.若传送带每次以不同的速度匀速运送该货物.
(1)若皮带不动,物体能否达到B端?若能,请求出达到B端速度VB
(2)当传送带的速度为多大时,物体运动到B端时恰好与传送带的速度相等?
(3)试在图2的背景方格上建立坐标系,画出货物在右岸上滑行的距离s随传送带速度平方v2变化的图象.
(1)若皮带不动,物体能否达到B端?若能,请求出达到B端速度VB
(2)当传送带的速度为多大时,物体运动到B端时恰好与传送带的速度相等?
(3)试在图2的背景方格上建立坐标系,画出货物在右岸上滑行的距离s随传送带速度平方v2变化的图象.

分析:(1)若皮带不动,物体在滑动摩擦力作用下做匀减速直线运动,根据位移速度公式求出到达右岸的速度即可判断;
(2)设传送带的速度为v,根据运动学基本公式即可求解;
(3)分三种情况进行讨论分析:一直匀减速运动,先匀减速后匀速或先匀加后匀速,一直匀加速运动,进而求出速度的平方与滑行位移的关系.
(2)设传送带的速度为v,根据运动学基本公式即可求解;
(3)分三种情况进行讨论分析:一直匀减速运动,先匀减速后匀速或先匀加后匀速,一直匀加速运动,进而求出速度的平方与滑行位移的关系.
解答:解:(1)若皮带不动,物体在滑动摩擦力作用下做匀减速直线运动,根据牛顿第二定律得:
a1=
=-2m/s2
根据匀减速运动位移速度公式得:
2a1L=vB2-v02
解得vB=2m/s>0
所以能到达B端,到B端速度VB=2m/s
(2)设传送带的速度为v,
若v<4m/s,则物体做匀减速运动,到达右端时速度恰好也为v,
则根据第一问可知此时v=2m/s
若v>4m/s,物体做匀加速运动,到达右端时速度恰好也为v,
则此时加速度为a2=2m/s2,根据位移速度公式有:
2a2L=v 2-v02
解得:v=2
m/s
(3)当传送带速度0≤v≤2时,物体做匀减速运动,到达右端的速度也为2m/s,
然后在右侧做匀减速运动,直到停止,根据牛顿第二定律得:
a3=
=-4m/s2
根据位移速度公式得:x1=
=
m=0.5m
当传送带速度2<v≤2
时,
物体离开传送带到达右端的速度与传送带速度相同,根据位移速度公式得:
x2=
=
当传送带速度v>2
m/s时物体一直做匀加速运动,此时加速度为a2,到达右端的速度为:
2a2L=v′2-v02
解得:v′=2
m/s
根据位移速度公式得:
x3=
=x3=
=3.5m
货物在右岸上滑行的距离s随传送带速度平方v2变化的图象如下图所示:

答:(1)能,到B端速度VB=2m/s;
(2)当传送带速度为v=2m/s或v=2
m/s时物体运动到B端时恰好与传送带的速度相等;
(3)如图所示.
a1=
| -μ1mg |
| m |
根据匀减速运动位移速度公式得:
2a1L=vB2-v02
解得vB=2m/s>0
所以能到达B端,到B端速度VB=2m/s
(2)设传送带的速度为v,
若v<4m/s,则物体做匀减速运动,到达右端时速度恰好也为v,
则根据第一问可知此时v=2m/s
若v>4m/s,物体做匀加速运动,到达右端时速度恰好也为v,
则此时加速度为a2=2m/s2,根据位移速度公式有:
2a2L=v 2-v02
解得:v=2
| 7 |
(3)当传送带速度0≤v≤2时,物体做匀减速运动,到达右端的速度也为2m/s,
然后在右侧做匀减速运动,直到停止,根据牛顿第二定律得:
a3=
| -μ2mg |
| m |
根据位移速度公式得:x1=
| 0-v2 |
| 2a3 |
| 0-4 |
| -8 |
当传送带速度2<v≤2
| 7 |
物体离开传送带到达右端的速度与传送带速度相同,根据位移速度公式得:
x2=
| 0-v2 |
| 2a3 |
| v2 |
| 8 |
当传送带速度v>2
| 7 |
2a2L=v′2-v02
解得:v′=2
| 7 |
根据位移速度公式得:
x3=
| 0-v′2 |
| 2a2 |
| 0-v′2 |
| 2a3 |
货物在右岸上滑行的距离s随传送带速度平方v2变化的图象如下图所示:

答:(1)能,到B端速度VB=2m/s;
(2)当传送带速度为v=2m/s或v=2
| 7 |
(3)如图所示.
点评:本题关键是对物体的运动情况分析清楚,然后根据牛顿第二定律、运动学公式列式求解,难度较大.

练习册系列答案
相关题目
 如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点),以v0=10m/s的初速度水平地滑上水平传送带,已知旅行包与皮带之间的动摩擦因数为μ=0.6.g取10m/s2,试讨论下列问题:
如图1所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点),以v0=10m/s的初速度水平地滑上水平传送带,已知旅行包与皮带之间的动摩擦因数为μ=0.6.g取10m/s2,试讨论下列问题: